ALUNOS TEM 1 ; TE 1 LER EM 22/03/16
Conjuntos e Conjuntos Numéricos
Aqui é só para vocês alunos LER como atividade de reforço.
TEORIA DOS CONJUNTOS
Conceitos de conjuntos
Tipos de conjunto
Tipos de conjunto
Existem diferentes tipos de conjuntos, seus nomes estão de acordo com a quantidade de elementos que eles agrupam.
O agrupamento de termos com características semelhantes é uma definição para a palavra conjunto. Os conjuntos recebem nomes de acordo com a quantidade de elementos que podem vir a ser agrupados.
Conjunto finito
Esse tipo de conjunto representa uma quantidade limitada de elementos. Por exemplo, o conjunto dos números naturais compreendidos entre 1 e 10 será representado da seguinte maneira: {x∊ N / 1 < x < 10} ou {2, 3, 4, 5, 6, 7, 8, 9}
Conjunto infinito
Apresenta uma quantidade infinita (ilimitada de termos). Por exemplo:
O conjunto dos reais é considerado um conjunto infinito, pois não possui fim.
O conjunto dos números inteiros também é considerado infinito.
Conjunto unitário
Esse conjunto é caracterizado por possuir apenas um único elemento. Por exemplo:
O conjunto dos números naturais compreendidos entre 0 e 2. Nesse caso existe somente um elemento, o 1. Representamos por {1}.
O conjunto dos números inteiros compreendidos entre –3 e –1. Entre os números –3 e –1 existe apenas o número inteiro –2. Portanto, a representação deste conjunto unitário é {–2}.
Conjunto Vazio
O conjunto vazio não possui nenhum elemento, a sua representação pode ser feita utilizando duas simbologias: { } ou Ø. Por exemplo:
O conjunto dos números naturais antecessores ao 0 (zero) é considerado vazio, pois nos números naturais não existe antecessor de zero.
O conjunto dos números fracionários existentes no conjunto dos números inteiros é considerado um conjunto vazio, pois não existem frações dentre os números inteiros.
Conjunto vazio: é um conjunto que não possui elementos. O conjunto vazio é representado por { } ou  .
.
Subconjuntos: quando todos os elementos de um conjunto A qualquer pertencem a um outro conjunto B, diz-se, então, que A é um subconjunto de B, ou seja
A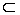 B. Observações:
B. Observações:
- Todo o conjunto A é subconjunto dele próprio, ou seja
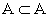 ;
;
- O conjunto vazio, por convenção, é subconjunto de qualquer conjunto, ou seja
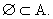
União de Conjuntos: dados os conjuntos A e B, define-se como união dos conjuntos A e B ao conjunto representado por 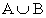 , formado por todos os elementos pertencentes a A ou B, ou seja:
, formado por todos os elementos pertencentes a A ou B, ou seja:
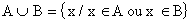
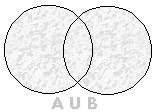
Intersecção de Conjuntos: dados os conjuntos A e B, define-se como intersecção dos conjuntos A e B ao conjunto representado por  , formado por todos os elementos pertencentes a A e B, simultaneamente, ou seja:
, formado por todos os elementos pertencentes a A e B, simultaneamente, ou seja:
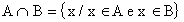
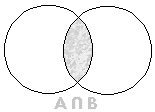
Diferença de Conjuntos: dados os conjuntos A e B, define-se como diferença entre A e B (nesta ordem) ao conjunto representado por A - B, formado por todos os elementos pertencentes a A, mas que não pertencem a B, ou seja
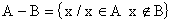
Número de subconjuntos de um conjunto: se um conjunto A possuir n elementos, então existirão 2n subconjuntos de A e representamos por P(A) =
2n
OPERAÇÕES COM CONJUNTOS
O agrupamento de termos com características semelhantes é uma definição para a palavra conjunto. Os conjuntos recebem nomes de acordo com a quantidade de elementos que podem vir a ser agrupados.
Conjunto finito
Esse tipo de conjunto representa uma quantidade limitada de elementos. Por exemplo, o conjunto dos números naturais compreendidos entre 1 e 10 será representado da seguinte maneira: {x∊ N / 1 < x < 10} ou {2, 3, 4, 5, 6, 7, 8, 9}
Conjunto infinito
Apresenta uma quantidade infinita (ilimitada de termos). Por exemplo:
O conjunto dos reais é considerado um conjunto infinito, pois não possui fim.
O conjunto dos números inteiros também é considerado infinito.
Conjunto unitário
Esse conjunto é caracterizado por possuir apenas um único elemento. Por exemplo:
O conjunto dos números naturais compreendidos entre 0 e 2. Nesse caso existe somente um elemento, o 1. Representamos por {1}.
O conjunto dos números inteiros compreendidos entre –3 e –1. Entre os números –3 e –1 existe apenas o número inteiro –2. Portanto, a representação deste conjunto unitário é {–2}.
Conjunto Vazio
O conjunto vazio não possui nenhum elemento, a sua representação pode ser feita utilizando duas simbologias: { } ou Ø. Por exemplo:
O conjunto dos números naturais antecessores ao 0 (zero) é considerado vazio, pois nos números naturais não existe antecessor de zero.
O conjunto dos números fracionários existentes no conjunto dos números inteiros é considerado um conjunto vazio, pois não existem frações dentre os números inteiros.
Conjunto finito
Esse tipo de conjunto representa uma quantidade limitada de elementos. Por exemplo, o conjunto dos números naturais compreendidos entre 1 e 10 será representado da seguinte maneira: {x∊ N / 1 < x < 10} ou {2, 3, 4, 5, 6, 7, 8, 9}
Conjunto infinito
Apresenta uma quantidade infinita (ilimitada de termos). Por exemplo:
O conjunto dos reais é considerado um conjunto infinito, pois não possui fim.
O conjunto dos números inteiros também é considerado infinito.
Conjunto unitário
Esse conjunto é caracterizado por possuir apenas um único elemento. Por exemplo:
O conjunto dos números naturais compreendidos entre 0 e 2. Nesse caso existe somente um elemento, o 1. Representamos por {1}.
O conjunto dos números inteiros compreendidos entre –3 e –1. Entre os números –3 e –1 existe apenas o número inteiro –2. Portanto, a representação deste conjunto unitário é {–2}.
Conjunto Vazio
O conjunto vazio não possui nenhum elemento, a sua representação pode ser feita utilizando duas simbologias: { } ou Ø. Por exemplo:
O conjunto dos números naturais antecessores ao 0 (zero) é considerado vazio, pois nos números naturais não existe antecessor de zero.
O conjunto dos números fracionários existentes no conjunto dos números inteiros é considerado um conjunto vazio, pois não existem frações dentre os números inteiros.
Subconjuntos: quando todos os elementos de um conjunto A qualquer pertencem a um outro conjunto B, diz-se, então, que A é um subconjunto de B, ou seja
A
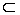 B. Observações:
B. Observações: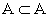 ;
;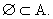

Intersecção de Conjuntos: dados os conjuntos A e B, define-se como intersecção dos conjuntos A e B ao conjunto representado por
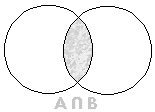
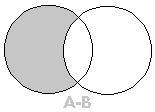
Diferença de Conjuntos: dados os conjuntos A e B, define-se como diferença entre A e B (nesta ordem) ao conjunto representado por A - B, formado por todos os elementos pertencentes a A, mas que não pertencem a B, ou seja

Número de subconjuntos de um conjunto: se um conjunto A possuir n elementos, então existirão 2n subconjuntos de A e representamos por P(A) =
2n
Exemplo 1:
Dados dois conjuntos A = {5,6,9,8}e B = {0,1,2,3,4,5}, se pedimos a interseção deles teremos:
A ∩ B = {5}, dizemos que A “inter” B é igual a 5.
Dados dois conjuntos A = {5,6,9,8}e B = {0,1,2,3,4,5}, se pedimos a interseção deles teremos:
A ∩ B = {5}, dizemos que A “inter” B é igual a 5.
Exemplo 2:
Dados os conjuntos B = {-3, -4, -5, -6} e C = {-7, -8, -9}, se pedirmos a interseção deles teremos:
B ∩ C = { } ou B ∩ C =.jpg) , então B e C são conjuntos distintos.
, então B e C são conjuntos distintos.
Dados os conjuntos B = {-3, -4, -5, -6} e C = {-7, -8, -9}, se pedirmos a interseção deles teremos:
B ∩ C = { } ou B ∩ C =
.jpg) , então B e C são conjuntos distintos.
, então B e C são conjuntos distintos.Exemplo 3:
Dados os conjuntos D = {1,2,3,4,5} e E = {3,4,5}. A interseção dos conjuntos ficaria assim:
E ∩ D = {3,4,5} ou E ∩ D = E, pode ser concluído também que
E
.jpg) D.
D..jpg)
União
Conjunto união são todos os elementos dos conjuntos relacionados.
Exemplo 1:
Dados os conjuntos A = { x | x é inteiro e -1 < x < 2} e
B = {1,2,3,4} a união desses dois conjuntos é : A U B = {0,1,2,3,4}
Exemplo 2:
Dados os conjuntos A = {1,2,3} e B = {1,2,3,4,5} a união desses conjuntos é:
A U B = {1,2,3,4,5}, nesse caso podemos dizer que A U B = B.
Diferença entre dois conjuntos.
Dados dois conjuntos A e B chama-se conjunto diferença ou diferença entre A e B o conjunto formado pelos elementos de A que não pertencem a B.
O conjunto diferença é representado por A – B.
Exemplo 1:
Exemplo 2:
Dados os conjuntos A = {1,2,3} e B = {1,2,3,4,5} a união desses conjuntos é:
A U B = {1,2,3,4,5}, nesse caso podemos dizer que A U B = B.
Diferença entre dois conjuntos.
Dados dois conjuntos A e B chama-se conjunto diferença ou diferença entre A e B o conjunto formado pelos elementos de A que não pertencem a B.
O conjunto diferença é representado por A – B.
Exemplo 1:
A = {1,2,3,4,5} e B = {3,4,5,6,7} a diferença dos conjuntos é:
A – B = {1,2}
Exemplo 2:
A = {1,2,3,4,5} e B = {8,9,10} a diferença dos conjuntos é:
A – B = {1,2,3,4,5}
Conjuntos Numéricos
Veja os conjuntos dos números naturais, inteiros, racionais, irracionais e reais.
Conjunto dos Números Naturais (N)
Um subconjunto importante de Ν é o conjuntoΝ*:
Ν*={1, 2, 3, 4, 5,…} ► o zero foi excluído do conjunto Ν.
Podemos considerar o conjunto dos números naturais ordenados sobre uma reta, como mostra o gráfico abaixo:
Conjunto dos números inteiros (Z)
O conjunto Ν é subconjunto de Z.
Temos também outros subconjuntos de Z:
Z* = Z - {0}
Z+ = conjunto dos inteiros não negativos = {0,1,2,3,4,5,…}
Z_ = conjunto dos inteiros não positivos = {0,-1,-2,-3,-4,-5,…}
Z+ = conjunto dos inteiros não negativos = {0,1,2,3,4,5,…}
Z_ = conjunto dos inteiros não positivos = {0,-1,-2,-3,-4,-5,…}
Observe que Z+ = Ν.
Podemos considerar os números inteiros ordenados sobre uma reta, conforme mostra o gráfico abaixo:
Conjunto dos números racionais (Q)
Os números racionais são todos aqueles que podem ser colocados na forma de fração (com o numerador e denominador 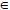 Z). Ou seja, o conjunto dos números racionais é a união do conjunto dos números inteiros com as frações positivas e negativas.
Z). Ou seja, o conjunto dos números racionais é a união do conjunto dos números inteiros com as frações positivas e negativas.
Então: 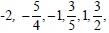 por exemplo, são números racionais.
por exemplo, são números racionais.
Exemplos:
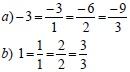
Assim, podemos escrever:

É interessante considerar a representação decimal de um número racional 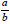 , que se obtém dividindo a por b.
, que se obtém dividindo a por b.
Exemplos referentes às decimais exatas ou finitas.
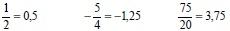
Exemplos referentes às decimais periódicas ou infinitas:
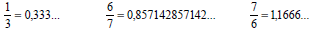
Toda decimal exata ou periódica pode ser representada na forma de número racional.
Conjunto dos números irracionais
Os números irracionais são decimais infinitas não periódicas, ou seja, os números que não podem ser escrito na forma de fração (divisão de dois inteiros). Como exemplo de números irracionais, temos a raiz quadrada de 2 e a raiz quadrada de 3:
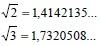
Um número irracional bastante conhecido é o número pi =3,1415926535…
Conjunto dos números reais (IR)
Dados os conjuntos dos números racionais (Q) e dos irracionais, definimos o conjunto dos números reais como:
O diagrama abaixo mostra a relação entre os conjuntos numéricos:
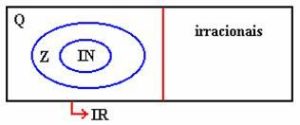
Portanto, os números naturais, inteiros, racionais e irracionais são todos números reais. Como subconjuntos importantes de IR temos:
IR* = IR-{0}
IR+ = conjunto dos números reais não negativo
IR_ = conjunto dos números reais não positivos
IR+ = conjunto dos números reais não negativo
IR_ = conjunto dos números reais não positivos
Obs: entre dois números inteiros existem infinitos números reais. Por exemplo:
Entre os números 1 e 2 existem infinitos números reais:
- 1,01 ; 1,001 ; 1,0001 ; 1,1 ; 1,2 ; 1,5 ; 1,99 ; 1,999 ; 1,9999 …
Entre os números 5 e 6 existem infinitos números reais:
- 5,01 ; 5,02 ; 5,05 ; 5,1 ; 5,2 ; 5,5 ; 5,99 ; 5,999 ; 5,9999 …


Exercício (Resolva em um rascunho sem precisar copiar)
1 - Dados os conjuntos A
= {1, 2}, B = {1, 2, 3, 4, 5}, C = {3, 4, 5}
e D = {0, 1, 2, 3, 4, 5}, classifique em verdadeiro (V) ou falso (F):
a) A Ì
B ( )
b) C Ì
A ( )
c) B Ì
D ( )
d) D Ì
B ( )
f) A Ì
D ( )
g) B Ì
C ( )
2 - Numa universidade são lidos
apenas dois jornais, X e Y. 80% dos alunos da mesma leem o jornal X e 60%, o
jornal Y. Sabendo-se que todo aluno é leitor de pelo menos um dos jornais,
assinale a alternativa que corresponde ao percentual de alunos que leem ambos:
a) 80%
b) 14%
c) 40%
d) 60%
e) 48%
b) 14%
c) 40%
d) 60%
e) 48%
3 - Numa outra pesquisa sobre a preferência em relação a dois jornais, foram consultadas 470 pessoas e o resultado foi o seguinte: 250 delas leem o jornal A, 180 leem o jornal B e 60 leem os jornais A e B. Pergunta-se:
a) Quantas pessoas leem apenas o jornal A?
b) Quantas pessoas leem apenas o jornal B?
c) Quantas pessoas leem jornais?
d) Quantas pessoas não lêem jornais?
4 - Determine a geratriz de cada uma das dízimas periódicas:
a) 0,262626...
b) 2,176176176...
c) 0,8474747...
d) 0,126666...
5 Dado que A = {2,4,6} e B = {2,3,5}. Obter n(A⋃B), ou seja, o número de elementos da união entre A e B.
(A) 2 (B) 3 (C) 4 (D) 5 (E) 6
6 - (UNESP) Se A = {2, 3, 5, 6, 7, 8}, B = {1, 2, 3, 6, 8} C = {1, 4, 6, 8}, então:
a) (A
– B) ∩ C = {1, 2}
b) (B
– A) ∩ C = {1}
c) (A
– B) ∩ C = {1}
d) (B
– A) ∩ C = {2}
e) n.d.a
SÓ CURIOSIDADE NÃO É PARA COPIAR TEM 1 E
TE 1 EM 22/03/16. LEIAM E VEJA COMO A
MATEMÁTICA TEM COISAS CURIOSAS
1 - Números amigáveis são pares de números onde um deles é a soma dos divisores do outro.
Por exemplo, os divisores de 220 são 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 e 110, cuja soma é 284.
Por outro lado, os divisores de 284 são 1, 2, 4, 71 e 142 e a soma deles é 220. Fermat descobriu também o par 17.296 e 18.416. Descartes descobriu o par 9.363.584 e 9.437.056
2 - O recorde de maior primo de Fermat generalizado conhecido: 16717632768+1, que tem 171153 dígitos foi descoberto por Yves Gallot (este é o oitavo maior primo conhecido atualmente, e maior primo conhecido que não é de mersenne
3 - São conhecidas 51539600000 casas decimais de Pi, calculadas por Y. Kamada e D. Takahashi, da Universidade de Tokio em 1997. Em 21/8/1998 foi calculada pelo projeto Pihex a 5000000000000a. casa binária de Pi.
4 - Pitágoras descobriu que existe outra forma de calcular potências: através da soma de números ímpares. Ele descobriu que n2 é igual a soma dos nprimeiros números naturais ímpares. Exemplo:
52 = 1+3+5+7+9 = 25
5 - OBS : 1089 é conhecido como o número mágico. Veja porque:
Escolha qualquer número de três algarismos distintos: por exemplo, 875.
Agora escreva este número de trás para frente e subtraia o menor do maior:
875 - 578 = 297
Agora escreva este número de trás para frente e subtraia o menor do maior:
875 - 578 = 297
Agora inverta também esse resultado e faça a soma:
297 + 792 = 1089 (o número mágico)
297 + 792 = 1089 (o número mágico)
Aviso: antes que você nos envie um e-mail dizendo que não funciona com determinados números, lembramos que devem ser usado três dígitos no cálculo. Exemplo:
574 - 475 = 099
099 + 990 = 1089
099 + 990 = 1089


.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)