Função

MATEMÁTICA  -  2016

FUNÇÃO

(Aluno(a)s TEM 1  e  TE1)  

PLANO CARTESIANO

 

René Descartes , (Nascimento: 1596  1650 França) foi um filósofo, físico e matemático francês.¹ Durante a Idade Moderna, também era conhecido por seu nome latino Renatus Cartesius.

O Plano Cartesiano foi criado pelo matemático René Descartes. Como ele associava a geometria à álgebra, esta foi a forma que ele criou para representar graficamente expressões algébricas.

A sua utilização mais simples é a de representarmos graficamente a localização de pontos em um determinado plano. Através dele também podemos representar um segmento de reta ou um triângulo, por exemplo.

O plano cartesiano é composto de duas retas perpendiculares e orientadas, uma horizontal e outra vertical.

Damos no nome de eixo x ou eixo das abscissas à reta horizontal. À vertical denominamos de eixo y ou eixo das ordenadas.

O Sistema de Coordenadas Cartesianas, mais conhecido como Plano Cartesiano, foi criado por René Descartes com o objetivo de localizar pontos.

René Descartes deve ser considerado um gênio da Matemática, pois relacionou a Álgebra com a Geometria, o resultado desse estudo foi a criação do Plano Cartesiano (Cartesiano em homenagem a René Descartes, cartesio). Essa fusão resultou na Geometria Analítica. Descartes obteve grande destaque nos ramos da Filosofia e da Física, sendo considerado peça fundamental na Revolução Científica, por várias vezes foi chamado de pai da Matemática moderna. Ele defendia que a Matemática dispunha de conhecimentos técnicos para a evolução de qualquer área de conhecimento. 

O Sistema de Coordenadas Cartesianas, mais comumente conhecido como Plano Cartesiano, consiste em dois eixos perpendiculares numerados, denominados abscissas (horizontal) e ordenada (vertical), que tem a característica de representar pontos no espaço.

Descartes utilizou o Plano Cartesiano no intuito de representar planos, retas, curvas e círculos através de equações matemáticas. Os estudos iniciais da Geometria Analítica surgiram com as teorias de René Descartes, que representavam de forma numérica as propriedades geométricas. A criação da Geometria Analítica por Descartes foi fundamental para a criação do Cálculo Diferencial e Integral pelos cientistas Isaac Newton e Leibniz. O Cálculo se dedica ao estudo das taxas de variação de grandezas e a acumulação de quantidades, sendo de grande importância na Física, Biologia e Química, no que diz respeito a cálculos mais complexos e detalhados.

Além do Cálculo e da Geometria Analítica, os estudos de René Descartes permitiram o desenvolvimento da Cartografia, ciência responsável pelos aspectos matemáticos ligados à construção de mapas.  

Localizando pontos no Plano Cartesiano:


A(4 ; 3) → x = 4 e y = 3

B(1 ; 2) → x = 1 e y = 2

C( –2 ; 4) → x = –2 e y = 4

D(–3 ; –4) → x = –3 e y = –4

E(3 ; –3) → x = 3 e y = –3

 

Geometria

O interesse de Descartes pela matemática surgiu cedo, no College de la Flèche, escola do mais alto padrão, dirigida por jesuítas, na qual ingressara aos oito anos de idade. Mas por uma razão muito especial e que já revelava seus pendores filosóficos: a certeza que as demonstrações ou justificativas matemáticas proporcionam. Aos vinte e um anos de idade, depois de frequentar rodas matemáticas em Paris (além de outras), já graduado em Direito, ingressa voluntariamente na carreira das armas, uma das poucas opções “dignas” que se ofereciam a um jovem como ele, oriundo da nobreza menor da França. Durante os quase nove anos que serviu em vários exércitos, não se sabe de nenhuma proeza militar realizada por Descartes.²

A geometria analítica de Descartes apareceu em 1637 no pequeno texto chamado Geometria, como um dos três apêndices do Discurso do Método, obra considerada o marco inicial da filosofia moderna. Nela, em resumo, Descartes defende o método matemático como modelo para a aquisição de conhecimentos em todos os campos.

O Plano Cartesiano é muito utilizado na construção de gráficos de funções, onde os valores relacionados à x constituem o domínio e os valores de y, a imagem da função. A criação do Sistema de Coordenadas Cartesianas é considerada uma ferramenta muito importante na Matemática, facilitando a observação do comportamento de funções em alguns pontos considerados críticos.

 Veja também o site http://pt.slideshare.net/suelenarthuralexandre/o-pensamento-cartesiano-descartes-e-suas-contribuiespptx-pronto-36974199

Função 

Definição: É nada mais que um tipo particular de relação que possuem uma propriedade específica.

Função é uma expressão matemática que relaciona dois 

valores pertencentes a conjuntos diferentes, mas com 

relações entre si. A lei de formação que intitula uma 

determinada função, possui três características básicas: 

domínio, contradomínio e imagem. Essas características 

podem ser representadas por um diagrama de flechas, isso 

facilitará o entendimento por parte do estudante. Observe: 

Dada a seguinte função f(x) = x + 1, e os conjuntos A(1, 2, 

3, 4, 5) e B(1, 2, 3, 4, 5, 6, 7). Vamos construir o diagrama 

de flechas:

Nessa situação, temos que: 

Domínio: representado por todos os elementos do conjunto 

A. 

(1, 2, 3, 4, 5) 

Contradomínio: representado por todos os elementos do 

conjunto B. 

(1, 2, 3, 4, 5, 6, 7) 

Imagem: representada pelos elementos do contradomínio 

(conjunto B) que possuem correspondência com o domínio 

(conjunto A). 

(2, 3, 4, 5, 6) 


O conjunto domínio possui algumas características 

especiais 

que definem ou não uma função. Observe: 


Todos os elementos do conjunto domínio devem possuir 

representação no conjunto do contradomínio. Caso isso não 

ocorra, a lei de formação não pode ser uma função. 

Função 

Não é uma função

Um único elemento do domínio não deve possuir duas 

imagens. 

Não é função 

Dois elementos diferentes do domínio podem possuir a 

mesma imagem. 

Não é Função 

 Restam elementos no conjunto domínio, que não foram 

associados ao conjunto imagem

.
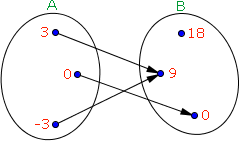
Para iniciarmos o estudo das funções vamos começar analisando a relação , cujo diagrama de flechas pode ser visto acima:
Observe que todos os elementos do conjunto A possuem uma flecha em direção a um único elemento do conjunto B.

Em outras palavras, não há no conjunto A qualquer elemento que não esteja associado a um elemento do conjunto B e os elementos de A estão associados a apenas um elemento de B.

Por possuir tal propriedade, dizemos que esta relação é uma função f de A em B representada por:

Domínio da Função

Ao conjunto A damos o nome de domínio da função.
O domínio é o conjunto de partida. Ele composto de todos os elementos do conjunto de partida.
Neste nosso exemplo o domínio da função f é representado por D(f) = { -3, 0, 3 }, ou seja, o domínio desta função contém todos os elementos do conjunto A.
Como supracitado, para que tenhamos uma função, todos os elementos do domínio devem estar associados a um e somente um dos elementos de B.

Contradomínio da Função

Ao conjunto B damos o nome de contradomínio da função.
O contradomínio é o conjunto de chegada. Ele composto de todos os elementos do conjunto de chegada.
Em nosso exemplo o contradomínio da função f é representado por CD(f) = { 0, 9, 18 }, isto é, o contradomínio desta função contém todos os elementos do conjunto B.

Segundo o conceito de função não é necessário que todos os elementos de B estejam relacionados aos elementos do domínio. Note que no conjunto B o elemento 18 não recebe nenhuma flecha, isto é, não está relacionado a qualquer elemento de A.
Uma outra coisa que deve ser observada é que em uma função os elementos do contradomínio podem receber mais de uma flechada, se associando, portanto, a mais de um elemento do domínio. Como exemplo temos o elemento 9 que está associado aos elementos do domínio -3 e 3.

Imagem da Função

A imagem da função dependendo do caso é o próprio contradomínio, ou então é um subconjunto seu.
Os elementos do conjunto imagem são todos os elementos do contradomínio que estão associados a algum elemento do domínio. No exemplo que estamos utilizando o conjunto imagem é representado por Im(f) = { 0, 9 }, pois 0 e 9 são todos os elementos do CD(f) que estão associados a algum elemento do D(f).
Em resumo para a função de exemplo temos:
Domínio da Função: D(f) = { -3, 0, 3 }
Contradomínio da Função: CD(f) = { 0, 9, 18 }
Conjunto Imagem da Função: Im(f) = { 0, 9 }
Nesta função o conjunto imagem é um subconjunto do contradomínio, pois o elemento 18 de B não está contido no conjunto imagem, por não estar associado a nenhum elemento do domínio.

Definição de uma Função

Esta função f de A em B, , é definida como:



Ou ainda como:



Veja também que representamos f(x) ou y em função de x. A variável f(x) ou y é chamada de variável dependente, pois depende de x, já a variável x é chamada de variável independente, pois independentemente de y, pode representar qualquer elemento do domínio.

A definição da função leva em conta tanto o domínio quanto do contradomínio, relacionando-os. O conjunto imagem Im(f), depende não só da regra de associação, no caso f(x) = x², como também do D(f) e do CD(f).

Exemplos de Relação que não é Função

 

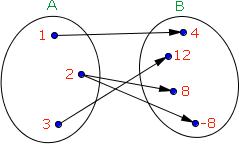
Observe o diagrama de flechas acima:
Ele não representa uma função de A em B, pois o elemento 2 do conjunto A possui duas imagens, -8 e 8, o que contraria o conceito de função.
Se apenas 8 ou -8 recebessem um flechada de 2, aí sim teríamos uma função.



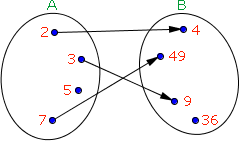
Agora vejamos este outro diagrama de flechas acima:
Veja que não há nenhum elemento do domínio que fleche mais de um elemento do contradomínio, mas ainda assim não estamos diante de uma função. Por quê?

Simplesmente porque o elemento 5 do conjunto A não possui uma imagem em B.

Zeros ou Raízes de uma Função

 
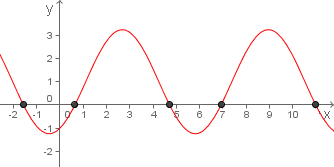
Olhe o gráfico da função ao lado e perceba que alguns dos seus pontos estão localizados sobre o eixo das abscissas.
A abscissa de cada um destes pontos é denominada zero da função ou raiz da função.

Todo elemento do domínio da função que tem como imagem o elemento 0, é uma raiz da função.
Os elementos do domínio que anulam a função são as suas raízes, isto significa dizer que dependendo da função, ela pode não possuir raízes reais, pois pode não existir no seu domínio nenhum elemento que a anule e sendo assim o seu gráfico nunca intercepta o eixo x, assim como também pode possuir infinitas raízes reais, pois o seu gráfico intercepta o eixo x infinitas vezes, já que podem existir infinitos elementos do seu domínio que tornem a função nula.

 Exercício  (COPIAR  E RESOLVER NO CADERNO, TE1 e  TEM 1 , ESSAS DUAS QUESTÕES   EM  22/03/16)

1 - Seja a função f : A → B dada pela lei de formação f(x) = 5x +2, sendo A = {–3, –2, –1, 0, 2} e B = {-14, -13, -8, -3, 2 , 12 , 15} . Determine o conjunto imagem dessa função.


2 - Dada a função f : R → R por f(x) = x² + 2x, determine o valor de f(2) + f(3) – f(1).

NÃO COPIAR             GRÁFICO É ASSUNTO DO ENEM, 

SPAECE  CONCURSOS ENTRE OUTROS  AQUI É SÓ PARA 

VOCÊS, TEM 1 E TE1  LEREM

Gráfico de segmentos

Observe a tabela que mostra a venda de livros de uma livraria no primeiro semestre de determinado ano:


O gráfico de segmento é utilizado principalmente para mostrar crescimento, decréscimo ou estabilidade.

Os gráficos são recursos utilizados para representar um 

fenômeno que possa ser mensurado, quantificado ou 

ilustrado de forma mais ou menos lógica. Assim como os 

mapas indicam uma representação espacial de um 

determinado acontecimento ou lugar, os gráficos apontam 

uma dimensão estatística sobre um determinado fato.

Por esse motivo, interpretar corretamente os gráficos 

disponibilizados em textos, notícias, entre outras situações, é 

de suma importância para compreender determinados 

fenômenos. Eles, geralmente, comparam informações 

qualitativas e quantitativas, podendo envolver também o 

tempo e o espaço.

Existe uma grande variedade de tipos de gráficos, dentre os 

quais podemos destacar os de coluna, em barras, pizza, 

área, linha e rede.

Gráficos de coluna

Juntamente aos gráficos em barra, são os mais utilizados. 

Indicam, geralmente, um dado quantitativo sobre diferentes 

variáveis, lugares ou setores e não dependem de 

proporções. Os dados são indicados na posição vertical, 

enquanto as divisões qualitativas apresentam-se na posição 

horizontal.

Gráficos em linhas

O gráfico de linha é utilizado para demonstrar uma 

sequência numérica de um certo dado ao longo do tempo. É 

indicado para demonstrar evoluções (ou regressões) que 

ocorrem em sequência para que o comportamento dos 

fenômenos e suas transformações seja observado.

Função do 1º grau  OU FUNÇÃO AFIM  -  PRÓXIMO ASSUNTO TEM1 E TE 1

O estudo das funções é importante, uma vez que elas podem ser aplicadas em diferentes circunstâncias: nas engenharias, no cálculo estatístico de animais em extinção, etc.

O significado de função é intrínseco à matemática, permanecendo o mesmo para qualquer tipo de função, seja ela do 1° ou do 2° grau, ou uma função exponencial ou logarítmica. Portanto, a função é utilizada para relacionar valores numéricos de uma determinada expressão algébrica de acordo com cada valor que a variável x assume.

 

Aplicações de uma Função de 1º grau

 

                                                                            
(Não precisa copiar)
















Exemplo 1

1 - Uma pessoa vai escolher um plano de saúde entre duas opções: A e B. 


Condições dos planos:


Plano A: cobra um valor fixo mensal de R$ 140,00 e R$ 20,00 por consulta num certo período.


Plano B: cobra um valor fixo mensal de R$ 110,00 e R$ 25,00 por consulta num certo período.

Temos que o gasto total de cada plano é dado em função do número de consultas x dentro do período pré – estabelecido.
Vamos determinar:


a) A função correspondente a cada plano.


b) Em qual situação o plano A é mais econômico; o plano B é mais econômico; os dois se equivalem.


2 - Um motorista de táxi cobra R$ 4,50 de bandeirada mais R$ 0,90 por quilômetro rodado. Sabendo que o preço a pagar é dado em função do número de quilômetros rodados, calcule o preço a ser pago por uma corrida em que se percorreu 22 quilômetros?


  Definição
 Chama-se função polinomial do 1º grau, ou função afim, a qualquer função f de IR em IR dada por uma lei da forma f(x) = ax + b, onde a e b são números reais dados e a0.
 Na função f(x) = ax + b, o número a é chamado de coeficiente de x e o número b é chamado termo constante.
 Veja alguns exemplos de funções polinomiais do 1º grau:

 f(x) = 5x - 3, onde a = 5 e b = - 3


 f(x) = -2x - 7, onde a = -2 e b = - 7


 f(x) = 11x, onde a = 11 e b = 0
Gráfico
    O gráfico de uma função polinomial do 1º grau,                 y = ax + b, com a0, é uma reta oblíqua aos eixos Ox e Oy.
    
Exemplo:

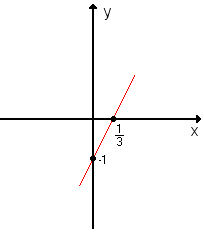
    Vamos construir o gráfico da função y = 3x - 1:
    Como o gráfico é uma reta, basta obter dois de seus pontos e ligá-los com o auxílio de uma régua:
    a)    Para   x = 0, temos   y = 3 · 0 - 1 = -1; portanto, um ponto é (0, -1).
    b)    Para   y = 0, temos   0 = 3x - 1; portanto, e outro ponto é .
    Marcamos os pontos (0, -1) e no plano cartesiano e ligamos os dois com uma reta.

x y 0 -1 0

 Exercício(NÃO, SÓ PARA TER UMA IDEIA  TE 1 e TEM 1  )

1 -Dois táxis têm preços dados por:

Táxi A: bandeirada a R$ 4,00, mais R$ 0,75 por quilômetro rodado;

Táxi B: bandeirada a R$ 3,00, mais R$ 0,90 por quilômetro rodado.
a)  Obtenha a expressão que fornece o preço de cada táxi (P_A­ e P_B) em função da distância  x  percorrida.

b)       Para que distâncias é vantajoso tomar cada táxi  A?

2 O valor de um carro novo é de R$9.000,00 e, com 4 anos de uso, é de R$4.000,00. Supondo que o preço caia com o tempo, segundo uma linha reta, o valor de um carro com 1 ano de uso é:

a) R$8.250,00         b) R$8.000,00        c) R$7.750,00          d) R$7.500,00     e) R$7.000,00

3. (FGV) Uma fábrica de bolsas tem um custo fixo mensal de R$5000,00. Cada bolsa fabricada custa R$25,00 e é vendida por R$45,00. Para que a fábrica tenha um lucro mensal de R$ 4000,00, ela deverá fabricar e vender mensalmente x bolsas. O valor de x é:

a) 300   b) 350        c) 400            d) 450                    e) 500

4 (FGV) Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8. Portanto, o valor de f(10) é:

a) 16          b) 17         c) 18             d) 19                  e) 20

5. (UFPE) Um provedor de acesso à Internet oferece dois planos para seus assinantes:

Plano A - Assinatura mensal de R$8,00 mais R$0,03 por cada minuto de conexão durante o mês.

Plano B - Assinatura mensal de R$10,00 mais R$0,02 por cada minuto de conexão durante o mês.

Acima de quantos minutos de conexão por mês é mais econômico optar pelo plano B?

a) 160                        b) 180                              c) 200             d) 220              e) 240

6. (FGV) Uma fábrica de camisas tem um custo mensal dado por C = 5000 + 15x, onde x é o número de camisas produzidas e vendidas por mês. Cada camisa é vendida por R$25,00. Atualmente, o lucro mensal é de R$2000,00. Para dobrar esse lucro, a fábrica deverá produzir e vender mensalmente:

a) o dobro do que produz e vende.          
b) 100 unidades a mais do que produz e vende.

c) 200 unidades a mais do que produz e vende.    

d) 300 unidades a mais do que produz e vende.

 NÃO  precisa copiar

1 - Como se pode repartir igualmente para duas pessoas, 8 litros de vinho que estão em uma vasilha maior, sabendo-se que as pessoas possuem somente duas vasilhas vazias, uma com capacidade para 5 litros e outra com capacidade para 3 litros.

2 - Há 10 litros de vinho em 3 vasilhas, com capacidades iguais a 5 litros, 3 litros e 7 litros, respectivamente. A primeira contem 4 litros de vinho, a segunda está vazia e a terceira contem 6 litros de vinho.

Como se pode repartir em duas partes iguais o vinho, usando apenas estas três vasilhas?

3 - Com três 5 e as operações elementares, obtenha:

1. O número 0;
2. O número 1;
3. O número 2;
4. O número 4;
5. O número 5;

4 - Construa um Quadrado Latino 3x3, que é um quadrado 3x3, de acordo com a figura em anexo, onde são colocados somente os algarismos 1, 2 e 3 nos quadradinhos de forma que a soma desses números, por linha, por coluna ou por diagonal seja sempre 6.

5 - Veja

6 -
Adaptado do livro O Homem Que Calculava, de autoria do grande brasileiro Malba Tahan.

• O problema dos quatro quatros é o seguinte:
•  
•  
• Escrever, com quatro quatros e alguns sinais matemáticos, uma expressão que seja igual a um número inteiro dado.
   
• Na expressão não pode aparecer (além dos quatro quatros) nenhum algarismo ou letra ou símbolo algébrico que envolva letras, tais como: logaritmo , limite , etc. Podem entretanto ser utilizados os símbolos de fatorial, (termial)* e raiz quadrada.
   
• (*) no enunciado original de Malba Tahan, o "termial" não é citado.

Afirmam os pacientes calculistas que é possível escrever, com quatro quatros, todos os números naturais de 0 a 100 e isto é verdadeiro, conforme demonstra a tabela abaixo.

Todos os números foram escritos utilizando-se as quatro operações fundamentais, raiz quadrada, fatorial e o termial.
Sobre o fatorial de um número natural, já sabemos que:
 
n! = n(n-1)(n-2)(n-3) ... . 2.1, para n maior ou igual a 2.
 
Exemplo.: 5! = 5.4.3.2.1 = 120

Sobre o termial, recebemos uma contribuição do visitante José Cássio Filardi, a qual reproduzimos a seguir:
 
"Professor: A função termial é bastante conhecida. Só não é comum o uso de um símbolo específico. De maneira semelhante ao fatorial, pode-se representá-la através de um somatório, ou seja: n? = 1 + 2 + 3 + 4 + ... + n , para n maior ou igual a 2.
 
Exemplo:  7? = 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28


A denominação "termial" deriva da expressão em inglês: "termial function" . Vide o livro - The Art of Computer Programming, segunda edição, vol. 1 / Fundamental Algorithms, Donald E. Knuth - Stanford University - Addison-Wesley Publishing Company ".
Então, com as informações do Filardi e outras, nem tanto, construímos esta tabela resumo:

N.º	Solução	N.º	Solução	N.º	Solução
0	44 – 44	35	4! + (44/4)	69	(4!/4)? + 4! + 4!
1	44/44	36	4! + 4 + 4 + 4	70	(4!+44) / 4
2	4/4 + 4/4	37	(4?)?- (4? +4+4)	71	(4?)? + 4? + (4! / 4)
3	(4+4+4)/4	38		72	(4!Ö4) / (4+4)
4		39		73	(4?)? + 4! - (4! / 4)
5		40		74	(44 / 4) + 4?
6		41		75	(4?)? + (4.4) + 4
7		42		76	4.4! - (4? + 4?)
8		43	44 - (4/4)	77	[(4!)? + 4 + 4] / 4
9		44	44 + 4 – 4	78	44 + 4! + 4?
10		45	44 + (4/4)	79	(4?)? - 4 + 4! + 4
11	4? + 44 - 4	46		80	(4.4 + 4).4
12		47	4! + 4! - (4/4)	81	(4?)? + (4.4) + 4?
13		48	(Ö4)Ö 4 + 44	82	4.4! - (4? + 4)
14		49	4! + 4! + 4/4	83	[(4!)? / 4] + (4 + 4)
15		50		84	(4! – 4).4 + 4
16		51	(4?)? - (4.4) / 4	85	(4?)? + 4! + (4!/4)
17	4!-(4!+4)/4	52	4!.4 – 44	86	(4?)? + (4!/4)? + 4?
18		53	(4?)? - [(4 + 4)] / 4	87	4! + (4?)? + 4 + 4
19		54	(44 / 4) - 4?	88	44 + 44
20	(4? + 4?).(4/4)	55	(4?)? . 44 - 4	89	(4?)? + 44 - 4?
21		56	4! + 4! + 4 + 4	90	4.4! - (4!/4)
22		57	(4?)? + [(4+4) / 4]	91	(4?)? + [4.(4?)] - 4
23	4!-4(4-4)	58	(4?)? + [4 - (4/4)]	92	44 + 4! + 4!
24		59	(4?)? + (4.4) / 4	93	(4?)? + 4! + 4! - 4?
25	4! + 4(4-4)	60		94	4.(4!/4)? + 4?
26		61	(4!/4)? + 4.4?	95	4!.4 – 4/4
27		62	4! + 4! + 4? + 4	96	4!.4 + 4 – 4
28		63	(44 – 4)/4	97	4!.4+4/4
29		64		98	{[(4!)? - 4]/4} + 4!
30		65	(4 + 44) / 4	99	(4?)? + 4.4? + 4
31		66	(4?)? + 4? + (4/4)	100	(4! + 4/4).4
32		67	4 + 4 + 4 + (4?)?
33		68	44/4 + 4
34		69	(4! /4)? + 4! + 4!

NOTA:  Considerando-se que o termial de um número natural n maior ou igual a 2, é o somatório de todos os números naturais de 1 a n.

Cozinhar um bolo

7 - Como medirias os 11 minutos que são 

necessários para cozinhar um bolo, com duas 

ampulhetas de 8 e 5 minutos respectivamente?

                     

8- Buscando água, uma rã caiu em um poço de 30 

metros de profundidade. Na sua busca por 

sobrevivência, a obstinada rã conseguia subir 3 

metros cada dia, sendo que a noite resbalava e 

descia 2 metros. Quantos dias a rã demorou para sair 

do poço?

9 - Dois pais e dois filhos foram pescar. Cada um pescou um peixe, sendo que ao todo foram pescados 3 peixes. Como isso é possível?

10 - Divida o vinho entre os viajantes

Dois amigos bêbados compraram 8 litros de vinho. Eles estavam caminhando, e na metade do caminho, decidem separar-se, repartindo antes o vinho igualmente. 

Para realizar as medidas há um barril de 8 litros (onde está o vinho), uma vasilha de 5 e outra de 3 litros. Como eles podem fazer para repartir igualmente o vinho?

10 - Uma garrafa com sua tampa custa R$ 1,10. Sabendo que a garrafa custa R$ 1,00 a mais que a tampa, qual é o preço da tampa da garrafa? E qual é o preço da garrafa?

Você acha fácil dobrar uma folha de papel? Que tal tentar dobrá-la 50 vezes?

Aqui está a folha...	Dobrando 1 vez...
Dobrando 2 vezes...	Dobrando 3 vezes...
Dobrando 4 vezes...	Dobrando 5 vezes...
Dobrando 6 vezes...	...

Você pode até conseguir dobrar 7 ou 8 vezes, mas nada além disso. Porém, por incrível que pareça, se você conseguisse dobrar a folha 50 vezes, ela apresentaria uma espessura aproximadamente igual à distância da Terra à Lua.

Observação: para dobrar uma folha 50 vezes ela deveria ter mais de 4.000.000 Km de comprimento!

11 - 

Vamos imaginar que dobramos um enorme 

pedaço de papel ao meio. Depois dobramos 

mais uma vez, e outra vez, e assim por diante. 

Quantas vezes conseguimos dobrar o nosso 

pedaço de papel?

.

Normalmente conseguimos dobrar uma folha 

A4 apenas 6 vezes e dificilmente se 

consegue dobrar um pedaço maior mais do 

que 7 vezes. Experimentem!

.
Mas vamos imaginar que conseguimos 

dobrar um pedaço de papel 51 vezes. No 

final 

qual seria a espessura do nosso papel? Dez 

centímetros? 50 centímetros? Um metro? 

Cinquenta metros? Um quilômetro?

.
A resposta é mais de 150.000.000 km! Sim, 

cento e cinquenta milhões de quilômetros! No 

final obteríamos uma torre que se estenderia 

para lá do Sol!
.
Quando dobramos o papel a primeira vez 

obtemos uma espessura duas vezes maior 

do que a da folha inicial. Quando dobramos 

a segunda vez será quatro vezes mais 

espesso. 

Cada vez que dobramos uma vez 

duplicamos a espessura em relação ao 

dobramento anterior. Depois dos primeiros 

dobramentos 

os números tornam-se imediatamente muito 

grandes. Vamos ver como:
.

Primeira dobra...2 folhas

Segunda dobra... 4 folhas

3ª - 8 folhas

4ª - 16 folhas

5ª - 32 folhas

6ª - 64 folhas

7ª - 128 folhas

8ª - 256 folhas

………….

40ª - 1.000.000.000.000 folhas

…………

50ª - 1.000.000.000.000.000 folhas 

(espessura=100.000.000 km)

51ª – Espessura = 200.000.000 km

.

E passamos o Sol!

.

(Distância da Terra ao Sol = 149.597.871 km 

                            Você sabia…

         

 O grande Leonard Euler afirmou que não há soluções 

inteiras positivas para a equação

 X⁴ + y⁴ + z⁴ = w⁴. Durante 200 anos ninguém conseguiu 

demonstrar isto. Parecia ser uma afirmação verdadeira 

uma vez que também ninguém pode provar que era falsa.

Entretanto, Noam Elkies da Universidade de Harvard 

trabalhando com um potente computador encontrou

2682440⁴+15365639⁴+18796760⁴ = 20615673⁴

A afirmação de Euler é falsa!

  Você sabia…

              pi  é   aproximadamente:

3,1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066…?