Estudar é importante para o desenvolvimento intelectual, social e profissional
- Estudar é importante não apenas para ter uma profissão e conseguir um emprego. Quanto mais conhecimentos você adquire, mais preparado está para viver em sociedade e enfrentar os desafios que surgem ao longo da vida.
O que é ser estudante?
Ser estudante é a busca constante de saberes, é o prazer de devorar livros pelo simples gosto das descobertas. Todo dia devemos entender que a maior escola é você mesmo. Quando você se recusa de buscar novas descobertas tem outros que não cansa de continuar lutando.
Um problema que resolve com a função logarítmica e com o uso de cálculo (curso superior) Leitura. Mínimo 50 minutos -
turma T.E 1 (24/09/15)
NÃO É PARA COPIAR
Observe um problema de aplicação de logaritmo
1 - O corpo de uma vítima de assassinato foi descoberto às 23 horas. O médico da polícia chegou às 23:30 e imediatamente tomou a temperatura do cadáver, que era de 34,8 graus. Uma hora mais tarde ele tomou a temperatura outra vez e encontrou 34,1 graus. A temperatura do quarto era mantida constante a 20 graus. Admitindo que a temperatura normal de uma pessoa viva é de 36,5 graus, estime a hora em que se deu a morte. Observe um problema de aplicação de logaritmo
APLICAÇÃO DA FUNÇÃO LOGARÍTMICA
Os alunos T.E 1 leem em 24/09/15
NÃO precisa copiar. Ver como existe muitas aplicações de logaritmo
1ª) A escala Richter foi desenvolvida por Charles
Richter e Beno Gutenberg, no intuito de medir a magnitude de um terremoto provocado
pelo movimento das placas tectônicas.
A magnitude (graus) é o logaritmo da medida das
amplitudes (medida por aparelhos denominados sismógrafos) das ondas produzidas
pela liberação de energia do terremoto.
A
fórmula utilizada é a seguinte:
M
= log A - log A0
onde
M é a magnitude,
A é a amplitude
máxima,
A0 é
uma amplitude de referência.
Para calcular a energia liberada por um terremoto, usamos a seguinte fórmula:
I = (2/3).log(E/E0)
Onde
I varia
de 0 a 9, E é a energia liberada em kW/h e E0
= 7.10-3kW/h
A intensidade do som
A classificação do som como forte ou
fraco está relacionada ao nível de intensidade sonora, medida em watt/m².
ESCALA DECIBEL: cálculo da quantidade de decibéis de um som, dado por  , onde I0 = 10-12 W/m2 e que é a menor intensidade do som captado pelo ouvido humano.
, onde I0 = 10-12 W/m2 e que é a menor intensidade do som captado pelo ouvido humano.
3ª) O pH de uma substância
NÃO precisa copiar
Logaritmo
Os logaritmos criados por John Napier e Jobst Burgi, e
posteriormente adaptados por Henry Briggs, possuem a
seguinte lei de formação:
logab = x, onde:
a = base do logaritmo
b = logaritmando
x = logaritmo
O logaritmo de um número b em uma base a é o expoente x
que se deve aplicar à base a para se ter o número b. Dessa
forma:
logab = x ↔ ax = b
Exemplos:
log39 = 2 , pois 32 = 9
log10100 =2, pois 102 = 100
log216 =2, pois 24 = 16
log981 =2, pois 92 = 81
Exemplos:
a) log100 = 2 porque 102 = 100.
b) log1000 = 3 porque 103 = 1000.
c) log2 = 0,3010 porque 100,3010 = 2.
d) log3 = 0,4771 porque 100,4771 = 3.
e) ln e = 1 porque e1 = e = 2,7183...
f) ln 7 = loge7
NÃO precisa copiar
Observação importante. log10 A = log A
A partir dessa definição podemos apresentar algumas
definições que auxiliarão no desenvolvimento de algumas
situações envolvendo logaritmo. Veja:
O logaritmo do número 1 em qualquer base sempre será
igual a 0.
** loga1 = 0, pois a0 = 1
O logaritmo de qualquer número a na própria base a será
igual a 1.
** logaa = 1, pois a1 = a
O logaritmo de uma potência da base é o expoente, em
qualquer base.
** logaam = m, pois m * logaa = m * 1 = m
A potência de base a e expoente logab é igual a b.
** alogab = b, pois logab = x → ax = b
Dois logaritmos são iguais, quando seus logaritmandos
forem iguais.
** logab = logac ↔ b = c
NÃO precisa copiar
tabela abaixo (Conhecida como tábua dos logaritmos)
TABELA DE LOGARITMOS DECIMAIS
| nº | log | nº | log | |
| 1 | 0 | 50 | 1,69897 | |
| 2 | 0,30103 | 51 | 1,70757 | |
| 3 | 0,477121 | 52 | 1,716003 | |
| 4 | 0,60206 | 53 | 1,724276 | |
| 5 | 0,69897 | 54 | 1,732394 | |
| 6 | 0,778151 | 55 | 1,740363 | |
| 7 | 0,845098 | 56 | 1,748188 | |
| 8 | 0,90309 | 57 | 1,755875 | |
| 9 | 0,954243 | 58 | 1,763428 | |
| 10 | 1 | 59 | 1,770852 | |
| 11 | 1,041393 | 60 | 1,778151 | |
| 12 | 1,079181 | 61 | 1,78533 | |
| 13 | 1,113943 | 62 | 1,792392 | |
| 14 | 1,146128 | 63 | 1,799341 | |
| 15 | 1,176091 | 64 | 1,80618 | |
| 16 | 1,20412 | 65 | 1,812913 | |
| 17 | 1,230449 | 66 | 1,819544 | |
| 18 | 1,255273 | 67 | 1,826075 | |
| 19 | 1,278754 | 68 | 1,832509 | |
| 20 | 1,30103 | 69 | 1,838849 | |
| 21 | 1,322219 | 70 | 1,845098 | |
| 22 | 1,342423 | 71 | 1,851258 | |
| 23 | 1,361728 | 72 | 1,857332 | |
| 24 | 1,380211 | 73 | 1,863323 | |
| 25 | 1,39794 | 74 | 1,869232 | |
| 26 | 1,414973 | 75 | 1,875061 | |
| 27 | 1,431364 | 76 | 1,880814 | |
| 28 | 1,447158 | 77 | 1,886491 | |
| 29 | 1,462398 | 78 | 1,892095 | |
| 30 | 1,477121 | 79 | 1,897627 | |
| 31 | 1,491362 | 80 | 1,90309 | |
| 32 | 1,50515 | 81 | 1,908485 | |
| 33 | 1,518514 | 82 | 1,913814 | |
| 34 | 1,531479 | 83 | 1,919078 | |
| 35 | 1,544068 | 84 | 1,924279 | |
| 36 | 1,556303 | 85 | 1,929419 | |
| 37 | 1,568202 | 86 | 1,934498 | |
| 38 | 1,579784 | 87 | 1,939519 | |
| 39 | 1,591065 | 88 | 1,944483 | |
| 40 | 1,60206 | 89 | 1,94939 | |
| 41 | 1,612784 | 90 | 1,954243 | |
| 42 | 1,623249 | 91 | 1,959041 | |
| 43 | 1,633468 | 92 | 1,963788 | |
| 44 | 1,643453 | 93 | 1,968483 | |
| 45 | 1,653213 | 94 | 1,973128 | |
| 46 | 1,662758 | 95 | 1,977724 | |
| 47 | 1,672098 | 96 | 1,982271 | |
| 48 | 1,681241 | 97 | 1,986772 | |
| 49 | 1,690196 | 98 | 1,991226 | |
| 99 | 1,995635 |
Veja as propriedades abaixo:
NÃO precisa copiar
NÃO precisa copiar
| 1°Propriedade: |
| 2° Propriedade: |
| 3° Propriedade: |
Uma maneira de visualizar esta propriedade, e tentar decorá-la mais facilmente, é imaginando a figura abaixo:
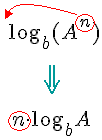
Veja as questões resolvidas ALUNO(A)S T.E 1 em 24/09/15 (Procure estudar essas questões resolvidas)
Não precisa copiar
Não precisa copiar
1 - Dados log2 = 0,301 e log3 = 0,477, determine o valor de
log12.
log12 → log12 = log(2 * 2 * 3) → log12 = log2 + log2 + log3
→ log12 = 0,301 + 0,301 + 0,477 → log 12 = 1,079
2 - Se log 8 = 0,903 e log 70 = 1,845, então log 14 é igual a:
a) 1,146
b) 1,164
c) 1,182
d) 1,208
e) 1,190
Solução:
Observe que 14 = 2x7. Portanto,
log 14 = log (2.7) = log 2 + log 7
Como log 8 = 0,903, poderemos escrever:
log 23 = 0,903 \ 3.log 2 = 0,903 \ log 2 = 0,903/3
log 2 = 0,301
Como log 70 = 1,845, poderemos escrever:
log 70 = log (7.10) = log 7 + log 10 = 1,845
Como o logaritmo decimal de 10 é igual a 1, ou seja,
log 10 = 1, vem imediatamente por substituição:
log 7 + 1 = 1,845 \ log 7 = 0,845.
Finalmente, log 14 = log (2.7) = log 2 + log 7
log 14 = 0,301 + 0,845 = 1,146log 14 = 1,146
3 - As indicações R1 e R2, na escala Ritcher, de dois terremotos estão relacionadas pela fórmula
R1 – R2 = log(M1/M2), onde M1 e M2 medem a energia liberada pelos terremotos sob a forma de ondas que se propagam pela crosta terrestre. Houve dois terremotos: um correspondente a R1 = 8 e outro correspondente a R2 = 6.
Então, a razão (M1/M2) vale:a) 100
b) 2
c) 4/3
d) 10
e) 1
R1 – R2 = log(M1/M2), onde M1 e M2 medem a energia liberada pelos terremotos sob a forma de ondas que se propagam pela crosta terrestre. Houve dois terremotos: um correspondente a R1 = 8 e outro correspondente a R2 = 6.
Então, a razão (M1/M2) vale:a) 100
b) 2
c) 4/3
d) 10
e) 1
Solução:
Decorre imediatamente do enunciado que:
8 – 6 = log (M1/M2) = 2.
Logo, (M1/M2) = 102 = 100.
8 – 6 = log (M1/M2) = 2.
Logo, (M1/M2) = 102 = 100.
a) a3
b) 5 a – 1
c) 1 + a/3
d) 2 a/3
e) 1 – a/3
Solução:
Podemos escrever:
log 23 = a \ 3.log 2 = a \ log 2 = a/3
log 23 = a \ 3.log 2 = a \ log 2 = a/3
Ora, 5 = 10/2 e, portanto,
log 5 = log(10/2) = log 10 – log 2 = 1 – a/3.log 5 = 1 – a/3
log 5 = log(10/2) = log 10 – log 2 = 1 – a/3.log 5 = 1 – a/3
Veja as equações resolvidas ALUNOS da turma T.E 1 em (24/09/15) não copiar


2 - Encontre a solução da equação


Solução: Pela definição de logaritmo temos:
5x + 2 = 33
5x + 2 = 27
5x = 27 – 2
5x = 25
x = 5
Portanto S = {5}.
3. Equação que é necessário fazer uma mudança de
incógnita.
5x + 2 = 33
5x + 2 = 27
5x = 27 – 2
5x = 25
x = 5
Portanto S = {5}.
3. Equação que é necessário fazer uma mudança de
incógnita.
Observe a resolução da equação -- NÃO COPIAR


Solução: Vamos fazer a seguinte mudança de incógnita

Substituindo na equação inicial, ficaremos com:

Tipo 4. Equações que utilizam as propriedades do logaritmo
ou mudança de base.

Substituindo na equação inicial, ficaremos com:

Tipo 4. Equações que utilizam as propriedades do logaritmo
ou mudança de base.
O conjunto solução da equação logaritmica =\frac{1}{2}) é:
é:
(A) {-1; 2}
(B) {-2; 1}
(C) {-2}
(D) {1}
(E) { }
(B) {-2; 1}
(C) {-2}
(D) {1}
(E) { }
Resolução
| Começamos aplicando apenas a equivalência fundamental: Agora é só aplicar a fórmula de Bhaskara. Chegando no valor de x devemos TESTAR AS SOLUÇÕES, como dito na única regra de resolução de equações logaritmicas. Verificação, para para Portanto, as duas respostas são válidas. E a alternativa correta é a letra "B" |
2) O número real x que satisfaz a equação =2x) é:
é:
(A) 
(B)
(C)
(D)
(E)
(B)
(C)
(D)
(E)
Resolução
| Aplicamos a equivalência fundamental: Agora caímos em uma equação exponencial do tipo II. Efetuando a troca de variáveis Aplicamos Bhaskara e chegamos em: Agora voltamos para x utilizando novamente a troca de variáveis feita inicialmente Agora devemos testar esta solução na equação original do enunciado. Substituindo este valor de x na equação: Aplicamos a 4° conseqüência da definição do logaritmo: Aplicamos a 3° propriedade operatória Resposta correta, letra "E". |
3) A equação
(A)
(B)
(C)
(D)
(E)
Resolução
| Esta equação já envolve um truquezinho, igual às equações exponenciais do tipo II. Começamos vendo que o 9 na equação pode virar 3². E aplicamos a 3° propriedade operatória: O pulo do gato vem agora. Devemos ver que os dois logaritmos envolvidos na equação acima são um o inverso do outro (1° consequência da mudança de base). Agora devemos mudar a variável. Efetuamos a troca Podemos multiplicar ambos os lados por y, ou efetuar MMC, tanto faz. Chegamos em: Aplicamos Bhaskara e chegamos em para y=2: para y=-1: O produto destes dois valores (como pedido no enunciado) é |
Gráfico da função logarítmica.
NÃO precisa copiar
NÃO precisa copiar
Observe com fica o gráfico da função logaritmica
Temos duas possibilidade
Para a > 1, temos o gráfico da seguinte forma:
Função crescente
.jpg)
Função crescente
.jpg)
Para 0 < a < 1, temos o gráfico da seguinte forma:
Função decrescente
.jpg)
Função decrescente
.jpg)
Características do gráfico da função logarítmica y = logax
O gráfico está totalmente à direita do eixo y, pois ela é definida para x > 0.
Intercepta o eixo das abscissas no ponto (1,0), então a raiz da função é x = 1.
Note que y assume todos as soluções reais, por isso dizemos que a Im (imagem) = R.
Através dos estudos das funções logarítmicas, chegamos à conclusão de que ela é uma função inversa da exponencial.
24/09/15. Copiar e resolver
1 - Resolva as equações logarítmica
a) log2 (x - 1) = 3 b) log3 (2x + 8) = 2 c) logx (64) = 2
2 - Sabendo que log2 = 0,30 e log3 = 0,47, determine o valor de:
a) log 120 b) log 12 c) log18
3 - Se log 3 = 0,47 e log 5 = 0,69 , determine o valor de:
a) log15 b) log 45 c) log75
Obs: As questões 3 e 4, se quiser podem ser verificada
consultando a tabela acima (Tábua dos logaritmos)
4 - Resolva as equações exponenciais
A) 5 x + 3 . 5 x + 2 . 5 x = 125
B) 2 3x – 2 . 8 x + 1 = 4 x – 1
FIM DA ATIVIDADE PARA COPIAR, ALUNOS(A)S T.E.1
5 - Qual o valor do montante produzido
por um capital de R$ 1.200,00,
aplicado no regime de juros simples a
uma taxa mensal de 2%, durante 10
meses?
Fim
1 -(ITA) Determine o valor de
1/log2(100!) + 1/log3(100!) + 1/log4(100!) + ... +
1/log100(100!)
Obs: ! é o fatorial. Ex. 3! = 3.2.1 = 6, 5! = 5.4.3.2.1 = 120
2 - Na compra de um aparelho obtive
desconto de 20% por ter feito o
pagamento à vista. Se paguei
R$ 96,00 reais pelo aparelho, qual era
seu preço original?
desafios, curiosidade e problemas de
Matemática para vocês leem e resolver só
como desafios
NÃO precisa copiar
1 - Como se pode repartir igualmente para duas pessoas, 8 litros de vinho que estão em uma vasilha maior, sabendo-se que as pessoas possuem somente duas vasilhas vazias, uma com capacidade para 5 litros e outra com capacidade para 3 litros.

2 - Há 10 litros de vinho em 3 vasilhas, com capacidades iguais a 5 litros, 3 litros e 7 litros, respectivamente. A primeira contem 4 litros de vinho, a segunda está vazia e a terceira contem 6 litros de vinho.

Como se pode repartir em duas partes iguais o vinho, usando apenas estas três vasilhas?
3 - Com três 5 e as operações elementares, obtenha:
- O número 0;
- O número 1;
- O número 2;
- O número 4;
- O número 5;
4 - Construa um Quadrado Latino 3x3, que é um quadrado 3x3, de acordo com a figura em anexo, onde são colocados somente os algarismos 1, 2 e 3 nos quadradinhos de forma que a soma desses números, por linha, por coluna ou por diagonal seja sempre 6.

5 - Veja

6 -
Adaptado do livro O Homem Que Calculava, de autoria do grande brasileiro Malba Tahan.
Todos os números foram escritos utilizando-se as quatro operações fundamentais, raiz quadrada, fatorial e o termial.
Sobre o fatorial de um número natural, já sabemos que:
n! = n(n-1)(n-2)(n-3) ... . 2.1, para n maior ou igual a 2.
Exemplo.: 5! = 5.4.3.2.1 = 120
Sobre o termial, recebemos uma contribuição do visitante José Cássio Filardi, a qual reproduzimos a seguir:
"Professor: A função termial é bastante conhecida. Só não é comum o uso de um símbolo específico. De maneira semelhante ao fatorial, pode-se representá-la através de um somatório, ou seja: n? = 1 + 2 + 3 + 4 + ... + n , para n maior ou igual a 2.
Exemplo: 7? = 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28
A denominação "termial" deriva da expressão em inglês: "termial function" . Vide o livro - The Art of Computer Programming, segunda edição, vol. 1 / Fundamental Algorithms, Donald E. Knuth - Stanford University - Addison-Wesley Publishing Company ".
Então, com as informações do Filardi e outras, nem tanto, construímos esta tabela resumo:
NOTA: Considerando-se que o
termial de um número natural n maior ou igual a 2, é o somatório de todos os números
naturais de 1 a n.
Adaptado do livro O Homem Que Calculava, de autoria do grande brasileiro Malba Tahan.
- O problema dos quatro quatros é o seguinte:
- Escrever, com quatro quatros e
alguns sinais matemáticos, uma
expressão que seja igual a um número inteiro dado.
- Na expressão não pode aparecer
(além dos quatro quatros) nenhum algarismo ou letra ou símbolo algébrico que
envolva letras, tais como: logaritmo , limite , etc. Podem entretanto ser utilizados
os símbolos de fatorial, (termial)* e raiz quadrada.
- (*) no enunciado original de Malba Tahan, o "termial" não é citado.
Todos os números foram escritos utilizando-se as quatro operações fundamentais, raiz quadrada, fatorial e o termial.
Sobre o fatorial de um número natural, já sabemos que:
n! = n(n-1)(n-2)(n-3) ... . 2.1, para n maior ou igual a 2.
Exemplo.: 5! = 5.4.3.2.1 = 120
Sobre o termial, recebemos uma contribuição do visitante José Cássio Filardi, a qual reproduzimos a seguir:
"Professor: A função termial é bastante conhecida. Só não é comum o uso de um símbolo específico. De maneira semelhante ao fatorial, pode-se representá-la através de um somatório, ou seja: n? = 1 + 2 + 3 + 4 + ... + n , para n maior ou igual a 2.
Exemplo: 7? = 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28
A denominação "termial" deriva da expressão em inglês: "termial function" . Vide o livro - The Art of Computer Programming, segunda edição, vol. 1 / Fundamental Algorithms, Donald E. Knuth - Stanford University - Addison-Wesley Publishing Company ".
Então, com as informações do Filardi e outras, nem tanto, construímos esta tabela resumo:
| N.º | Solução | N.º | Solução | N.º | Solução |
| 0 | 44 – 44 | 35 | 4! + (44/4) | 69 | (4!/4)? + 4! + 4! |
| 1 | 44/44 | 36 | 4! + 4 + 4 + 4 | 70 | (4!+44) / 4 |
| 2 | 4/4 + 4/4 | 37 | (4?)?- (4? +4+4) | 71 | (4?)? + 4? + (4! / 4) |
| 3 | (4+4+4)/4 | 38 | 72 | (4!Ö4) / (4+4) | |
| 4 | 39 | 73 | (4?)? + 4! - (4! / 4) | ||
| 5 | 40 | 74 | (44 / 4) + 4? | ||
| 6 | 41 | 75 | (4?)? + (4.4) + 4 | ||
| 7 | 42 | 76 | 4.4! - (4? + 4?) | ||
| 8 | 43 | 44 - (4/4) | 77 | [(4!)? + 4 + 4] / 4 | |
| 9 | 44 | 44 + 4 – 4 | 78 | 44 + 4! + 4? | |
| 10 | 45 | 44 + (4/4) | 79 | (4?)? - 4 + 4! + 4 | |
| 11 | 4? + 44 - 4 | 46 | 44 - Ö4 + 4 | 80 | (4.4 + 4).4 |
| 12 | 47 | 4! + 4! - (4/4) | 81 | (4?)? + (4.4) + 4? | |
| 13 | 48 | (Ö4)Ö 4 + 44 | 82 | 4.4! - (4? + 4) | |
| 14 | 49 | 4! + 4! + 4/4 | 83 | [(4!)? / 4] + (4 + 4) | |
| 15 | 50 | 44 + Ö4 + 4 | 84 | (4! – 4).4 + 4 | |
| 16 | 51 | (4?)? - (4.4) / 4 | 85 | (4?)? + 4! + (4!/4) | |
| 17 | 4!-(4!+4)/4 | 52 | 4!.4 – 44 | 86 | (4?)? + (4!/4)? + 4? |
| 18 | 53 | (4?)? - [(4 + 4)] / 4 | 87 | 4! + (4?)? + 4 + 4 | |
| 19 | 54 | (44 / 4) - 4? | 88 | 44 + 44 | |
| 20 | (4? + 4?).(4/4) | 55 | (4?)? . 44 - 4 | 89 | (4?)? + 44 - 4? |
| 21 | 56 | 4! + 4! + 4 + 4 | 90 | 4.4! - (4!/4) | |
| 22 | 57 | (4?)? + [(4+4) / 4] | 91 | (4?)? + [4.(4?)] - 4 | |
| 23 | 4!-4(4-4) | 58 | (4?)? + [4 - (4/4)] | 92 | 44 + 4! + 4! |
| 24 | 59 | (4?)? + (4.4) / 4 | 93 | (4?)? + 4! + 4! - 4? | |
| 25 | 4! + 4(4-4) | 60 | 4Ö4 .4 – 4 | 94 | 4.(4!/4)? + 4? |
| 26 | 61 | (4!/4)? + 4.4? | 95 | 4!.4 – 4/4 | |
| 27 | 62 | 4! + 4! + 4? + 4 | 96 | 4!.4 + 4 – 4 | |
| 28 | 63 | (44 – 4)/4 | 97 | 4!.4+4/4 | |
| 29 | 64 | 4(4 - Ö4) . 4 | 98 | {[(4!)? - 4]/4} + 4! | |
| 30 | 65 | (4 + 44) / 4 | 99 | (4?)? + 4.4? + 4 | |
| 31 | 66 | (4?)? + 4? + (4/4) | 100 | (4! + 4/4).4 | |
| 32 | 67 | 4 + 4 + 4 + (4?)? | |||
| 33 | 68 | 44/4 + 4 | |||
| 34 | 69 | (4! /4)? + 4! + 4! |
Cozinhar um bolo
7 - Como medirias os 11 minutos que são
necessários para cozinhar um bolo, com duas
ampulhetas de 8 e 5 minutos respectivamente?



8- Buscando água, uma rã caiu em um poço de 30
metros de profundidade. Na sua busca por
sobrevivência, a obstinada rã conseguia subir 3
metros cada dia, sendo que a noite resbalava e
descia 2 metros. Quantos dias a rã demorou para sair
do poço?

9 - Dois pais e dois filhos foram pescar. Cada um pescou um peixe, sendo que ao todo foram pescados 3 peixes. Como isso é possível?
Dois amigos bêbados compraram 8 litros de vinho. Eles estavam caminhando, e na metade do caminho, decidem separar-se, repartindo antes o vinho igualmente.
Para realizar as medidas há um barril de 8 litros (onde está o vinho), uma vasilha de 5 e outra de 3 litros. Como eles podem fazer para repartir igualmente o vinho?

10 - Uma garrafa com sua tampa custa R$ 1,10. Sabendo que a garrafa custa R$ 1,00 a mais que a tampa, qual é o preço da tampa da garrafa? E qual é o preço da garrafa?

Você acha fácil dobrar uma folha de papel? Que tal tentar dobrá-la 50 vezes?
espesso.
Aqui está a folha... | Dobrando 1 vez... |
Dobrando 2 vezes... | Dobrando 3 vezes... |
Dobrando 4 vezes... | Dobrando 5 vezes... |
Dobrando 6 vezes... | ... |
Você pode até conseguir dobrar 7 ou 8 vezes, mas nada além disso. Porém, por incrível que pareça, se você conseguisse dobrar a folha 50 vezes, ela apresentaria uma espessura aproximadamente igual à distância da Terra à Lua.
Observação: para dobrar uma folha 50 vezes ela deveria ter mais de 4.000.000 Km de comprimento!
11 -
Vamos imaginar que dobramos um enorme
pedaço de papel ao meio. Depois dobramos
mais uma vez, e outra vez, e assim por diante.
Quantas vezes conseguimos dobrar o nosso
pedaço de papel?
.
Normalmente conseguimos dobrar uma folha
A4 apenas 6 vezes e dificilmente se
consegue dobrar um pedaço maior mais do
que 7 vezes. Experimentem!
.
Mas vamos imaginar que conseguimos
Mas vamos imaginar que conseguimos
dobrar um pedaço de papel 51 vezes. No
final
final
qual seria a espessura do nosso papel? Dez
centímetros? 50 centímetros? Um metro?
Cinquenta metros? Um quilômetro?
.
A resposta é mais de 150.000.000 km! Sim,
A resposta é mais de 150.000.000 km! Sim,
cento e cinquenta milhões de quilômetros! No
final obteríamos uma torre que se estenderia
para lá do Sol!
.
Quando dobramos o papel a primeira vez
.
Quando dobramos o papel a primeira vez
obtemos uma espessura duas vezes maior
do que a da folha inicial. Quando dobramos
a segunda vez será quatro vezes mais
do que a da folha inicial. Quando dobramos
a segunda vez será quatro vezes mais
espesso.
Cada vez que dobramos uma vez
duplicamos a espessura em relação ao
dobramento anterior. Depois dos primeiros
dobramentos
duplicamos a espessura em relação ao
dobramento anterior. Depois dos primeiros
dobramentos
os números tornam-se imediatamente muito
grandes. Vamos ver como:
.
.
Primeira dobra...2 folhas
Segunda dobra... 4 folhas
3ª - 8 folhas
4ª - 16 folhas
5ª - 32 folhas
6ª - 64 folhas
7ª - 128 folhas
8ª - 256 folhas
………….
40ª - 1.000.000.000.000 folhas
…………
50ª - 1.000.000.000.000.000 folhas
(espessura=100.000.000 km)
51ª – Espessura = 200.000.000 km
.
E passamos o Sol!
.
(Distância da Terra ao Sol = 149.597.871 km
X4 + y4 + z4 = w4. Durante 200 anos ninguém conseguiu
demonstrar isto. Parecia ser uma afirmação verdadeira
uma vez que também ninguém pode provar que era falsa.
Entretanto, Noam Elkies da Universidade de Harvard
trabalhando com um potente computador encontrou
Você sabia…
Você sabia…
O grande Leonard Euler afirmou que não há
soluções
inteiras positivas para a equação
inteiras positivas para a equação
X4 + y4 + z4 = w4. Durante 200 anos ninguém conseguiu
demonstrar isto. Parecia ser uma afirmação verdadeira
uma vez que também ninguém pode provar que era falsa.
Entretanto, Noam Elkies da Universidade de Harvard
trabalhando com um potente computador encontrou
26824404+153656394+187967604 = 206156734
A afirmação de Euler é falsa!
Você sabia…
pi é aproximadamente:
3,1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066…?