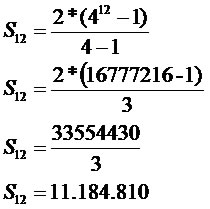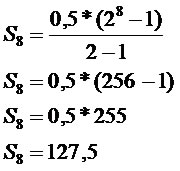Progressão Geométrica
T.E.1 - Ler a teoria
Dizemos que uma sequência numérica constitui uma progressão geométrica quando, a partir do 2º termo, o quociente entre um elemento e seu antecessor for sempre igual. Observe a sequência:
(2, 4, 8, 16, 32, 64,...), dizemos que ela é uma progressão geométrica, pois se encaixa na definição dada.
4 : 2 = 2
8 : 4 = 2
16 : 8 = 2
32 : 16 = 2
64 : 32 = 2
O termo constante da progressão geométrica é denominado razão.
Muitas situações envolvendo sequências são consideradas PG, dessa forma, foi elaborada uma expressão capaz de determinar qualquer elemento de uma progressão geométrica. Veja:
a2 = a1 * q
a3 = a1 * q2
a5 = a1 * q4
a10 = a1 * q9
a50 = a1*q49
a100 = a1*q99
Com base nessa sequencias, temos
.jpg)
Olhe a aplicação da P.G
Juros compostos e progressões geométricas
A maioria das operações financeiras efetuadas nos dias de hoje utiliza juros compostos para remunerar um capital. Para ilustrar, suponha, por exemplo, que uma pessoa aplicou R$ 1.000,00 em renda fixa a uma taxa de 20% ao ano. O montante M1, obtido após um ano de aplicação, é calculado adicionando-se ao capital aplicado os juros do período, ou seja:
M1 = 1.000,00 + 0,20 . 1.000,00, ou
M1 = 1.000,00 . (1+ 0,20)
M1 = 1.000,00 . 1,20
M1 = 1.200,00
Observe que, para aumentar uma quantia em 20%, basta multiplicá-la por 1,20. Dessa forma, o montante após dois anos é igual ao valor do montante após uma ano multiplicado por 1,20:
M2 = M1 . 1,20
M2 = 1.200,00 . 1,20
M2 = 1.440,00
O montante após três anos é igual ao montante após 2 anos multiplicado por 1,20:
M3 = M2 . 1,20
M3 = 1.440,00 . 1,20
M3 = 1.728,00
Procedendo da mesma forma, podemos concluir que a seqüência formada pelos valores dos montantes, ano a ano e com base no aplicado inicialmente, constitui-se numa PG cujo primeiro termo é igual a R$ 1.000,00 e cuja razão é igual a 1,20. Assim, teremos a seguinte sequencia:
(1.000,00 ; 1.200,00 ; 1.440,00 ; 1.728,00; ...)
Para estudarmos o modelo de variação de uma capital em um regime de capitalização composta C, aplicado a uma taxa mensal de i%, durante t meses. O montante produzido pelo primeiro mês será:
M1 = C. (1+i)
O montante produzido até o segundo mês é igual ao montante produzido no primeiro mês multiplicado por (1+i)
M2 = M1 . (1+i)
M2 = C . (1+i) (1+i)
M2 = C . (1+i)2
Dessa forma temos:
M3 = C . (1+i)3
M4 = C . (1+i)4
M5 = C . (1+i)5
Assim, o montante produzido até o mês t será dado por:
M(t) = C . (1+i)t
Essa última fórmula é utilizada para calcular o montante em uma aplicação de juros compostos, dados o capital C, a taxa de juros i e o prazo da aplicação t. A taxa de juros i deve referir-se a mesma unidade de tempo utilizada para o período t, ou seja, se a taxa for em 15% ao ano, por exemplo, o prazo de tempo deve ser considerado em anos.
Aplicação da fórmula
Exemplo 1 (Não copiar)
Em uma progressão geométrica, temos que o 1º termo equivale a 4 e a razão igual a 3. Determine o 8º termo dessa PG.
a8 = 4 * 37
a8 = 4 * 2187
a8 = 8748
O 8º termo da PG descrita é o número 8748.
Exemplo 2 (Resolvido)
Dada a PG (3, 9, 27, 81, ...), determine o 20º termo.
a20 = 3 * 319
a20 = 3 * 1.162.261.467
a20 = 3.486.784.401
Exercício (T.E.1 - copiar e resolver em 08/12/14)
1 - Determine o décimo termos da P.G. (2, 6, 18, 54...). .
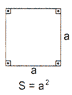
2 - No depósito da construção civil, encontra-se várias tábuas iguais. Elas deverão ser empilhadas respeitando a seguinte ordem: uma tábua na primeira vez e, em cada uma das vezes seguintes, tantas quantas já estejam na pilha. Por exemplo:
Determine a quantidade de tábuas empilhadas na 12ª pilha.
3 - O carro do Fernando, cujo preço à vista é R$ 24 000,00, pode ser adquirido dando-se uma entrada e o restante em 5 parcelas que se encontram em progressão geométrica. Um cliente que optou por esse plano, ao pagar a entrada, foi informado que a segunda parcela seria de R$ 4 000,00 e a quarta parcela de R$ 1 000,00. Quanto esse cliente pagou de entrada na aquisição desse carro?
copiar a fórmula da soma T.E. 1 em 08/12/14
7 – Soma dos n primeiros termos de uma P.G
Considerando (an) como uma P.G. de razão q e Sn a soma dos n primeiros termos, temos:
Não copiar
Ex1- Determine a soma dos doze primeiros elementos da progressão geométrica (2, 8, 32, 128, ...).
a1: 2 q (razão): 8 : 2 = 4 n: 12
2 - Uma pessoa resolve guardar um dinheiro obedecendo a uma progressão geométrica de razão 2. Considerando que no primeiro mês ela irá poupar R$ 0,50, qual será o valor poupado no oitavo mês e o total guardado no período?
Valor guardado no 8º mês.
a
n = a
1*q
n–1
a
8 = 0,5*2
8–1
a
8 = 0,5*2
7
a
8 = 0,5*128
a
8 = 64
No oitavo mês ela irá poupar R$ 64,00.
Total poupado
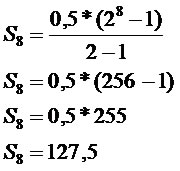
A quantia poupada no tempo determinado é de R$ 127,50.
Exercício (copiar e resolver T.E.1)
1 - Calcule:
a) a soma dos cinco primeiros termos da P.G. (2, 6, 18, ...)
b) a soma dos seis primeiros termos da P.G. (4 , 8 , 16 , ...);
c) a soma dos 10 primeiros termos da P.G. (1 , 2, 4, 8, 16, ...).
2 - Uma moça seria contratada como balconista para trabalhar de segunda a sábado nas duas últimas semanas que antecederiam o Natal. O patrão ofereceu R$ 1,00 pelo primeiro dia de trabalho e nos dias seguintes o dobro do que ela recebera no dia anterior. A moça recusou o trabalho. Se ela tivesse aceito a oferta, quanto teria recebido pelos 12 dias de trabalho?.
Obs: Os alunos do T.E. 1 deve copiar e resolver essas questões no caderno pois o Professor irá corrigir essa atividade valendo ponto.
Terminando a resolução (T.E.1) os alunos podem acessar o site www.educandusweb.com.br/ewce/portal login teste.teste7 senha 0312 e ver a apresentação dos conteúdos de P.G e P.A.
Curiosidade (Não copiar)

Johann Friederich Carl Gauss nasceu em Brunswick, Alemanha. De família humilde mas com o incentivo de sua mãe obteve brilhantismo em sua carreira. Estudando em sua cidade natal, certo dia quando o professor mandou que os alunos somassem os números de 1 a 100, imediatamente Gauss achou a resposta - 5050 - aparentemente sem cálculos. Supõe-se que já aí houvesse descoberto a fórmula de uma soma de uma progressão aritmética.
Johann Friedrich Carl Gauss (Alemão 1777), foi um matemático, astrônomo e físico alemão que contribuiu muito em diversas áreas da ciência, dentre elas a teoria dos números, estatística, análise matemática, geometria diferencial, geodésia, geofísica, astronomia e óptica.
1 - Um cachorro persegue um coelho. A velocidade do coelho é 1/10 da velocidade do cachorro.
A distância que os separa é de 100 metros. Nessas condições, quando o cachorro vencer os 100 metros, o coelho terá corrido 1/10 do que percorreu o cachorro e ficará 10 metros a sua frente. Quando o cachorro correr esses 10 metros, o coelho terá percorrido 1/10 dessa distância e estará 1 metro a sua frente. Quando o cachorro correr esse metro, o coelho terá corrido 10 centímetros, e assim por diante. Esse raciocínio pode levar muita gente a pensar que o cachorro nunca alcançará o coelho. Assim também pensou o coelho. Azar dele.
Com os recursos estudados é possível determinar em que ponto o cachorro alcançará o coelho. E, então, quantos metros ele deverá correr para alcançar o coelho?
 1) Quanto é 15% de 80?
1) Quanto é 15% de 80?







.jpg)