A função modular tem várias aplicações no cotidiano, como por exemplo a aplicação em comparação das temperaturas entre duas ou mais cidade, na Física, na Química na Geografia entre outras.
Todos os alunos deverão ler a teoria e depois copiar e resolver as atividades.
Para entender função modular - tema que cai nos vestibulares e no Enem - devemos compreender o que é módulo. Em seguida, através de exercícios, resolveremos algumas equações modulares e falaremos sobre a função modular:
O que muda ao inserirmos um módulo à função? Assunto mais adiante
Módulo
Antes de falar da função modular, vamos relembrar a definição e como calcular o módulo de um número. O módulo é a distância de um determinado número até o zero. Por exemplo, o módulo de 13 é a distância entre o 13 e o 0. Para nos deslocarmos do 13 ao 0, andaremos 13 unidades. Portanto, o módulo de 13 é igual a 13. Ou ainda: |13| = 13. Sendo assim, qual será o módulo de -13? Bem, a distância do -13 ao zero é também de 13 unidades. Então, |-13| = 13.
Módulo de um número realO módulo ou valor absoluto de um número real x é representado por |x|, que lemos: módulo de x.
1º - Se x for um número real positivo o módulo de x será o próprio x.
2º - Se x for um número real negativo o módulo de x será o x positivo.
Resumindo | - x | = x
| x | = x
Obs: O módulo pode ser interpretado como a distância, na reta real, de um número real x a origem (zero)
Considere a reta real:
Chamamos a distância de um ponto da reta à origem (distância do ponto até o zero) de módulo ou valor absoluto.
Assim, a distância do ponto 4 à origem é 4. Dizemos que o módulo de 4 é igual a 4. E representamos por |4| = 4
Da mesma forma, a distância do ponto -2 à origem é 2, ou seja, o módulo de -2 é 2, pois não há sentido em considerarmos distâncias negativas. Assim: |-2| = 2
Exemplos:
|3| = 3 |-18| = 18 |-20| = 20 |30| = 30
|-7| = 7 |0| = 0 |-100| = 100
a) |-3| = 3 b) |-8| = 8 c) |7| = 7 d) |10| = 10
1ª Atividade:
1 - Calcule o valor de cada expressão modular:
a) |-10 - 20 - 30| b) | -3 + 4 - 5 + 6 - 7|
2 - Determine:
a) |-4 + 8| + |-10 + 20| b) | 9 - 10 + 11| + | -7 + 6 |
3 - Seja a função modular f: R em R definida por f(x) = |2x - 10|, calcule
a) f(-3) b) f(-5)
4 - Seja f(x) = | x - 1 | + | x - 3 |, determine o valor de:
a) f(-3) b) f(-11)
5 -A estrada que liga Recife a Caruaru tem 240 km de extensão e será recuperada em três etapas. Na primeira etapa, será recuperado 1/6 da estrada e na segunda etapa 1/4 da estrada. Quantos quilômetros será recuperada na terceira etapa?
6 - A idade de um pai é o quádruplo da idade de seu filho. Daqui a cinco anos, a idade do pai será o triplo da idade do filho. Qual é a idade atual de cada um?
Propriedades do Módulo de Números Reais
1º) Para quaisquer valores reais de x temos as seguintes propriedades:
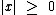
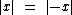
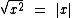
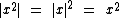
2º) Para a e b reais temos as seguintes propriedades:
a)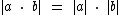
b)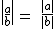 para
para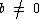
c)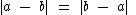

Gráfico de uma função modular: f(x) = | x |
Gráfico da função modular: f(x) = | x | x | y
Observe: x = -2 temos f(x) = 2, -2 | 2
x = -1 temos f(x) = 1, -1 | 1
x = 1 temos f(x) = 1 0 | 0 (raiz)
x = 2 temos f(x) = 2 1 | 1
2 | 2

Observe o esboço do gráfico da função f(x) = |2x + 6|
1º -Raiz da equação 2x + 6 = 0, temos 2x = -6 teremos x = -3 Para x = -3 temos f(x) = 0
x = -4 temos f(x) = 2 x | y
x = -1 temos f(x) = 4 -5 | 4
x = 0 temos f(x) = 6 -4 | 2
-3 | 0
-2 | 2
-1 | 4
 (Foto: Colégio EEEP Antônio Valmir da SilvaVamos esboçar o gráfico de g(x) = | x² - 5x + 4|:
(Foto: Colégio EEEP Antônio Valmir da SilvaVamos esboçar o gráfico de g(x) = | x² - 5x + 4|:
 (Foto: EEEP Antônio Valmir da Silva)
(Foto: EEEP Antônio Valmir da Silva)
 (Foto: EEEP Antônio Valmir da Silva)
(Foto: EEEP Antônio Valmir da Silva)
Veja o gráfico da função f(x) = |x² - 4| (legal)
Raízes são x² - 4 = 0, temos que x² = 4 ou x = -2 e x = 2 (pontos no eixo x)
x | y x | y
-4 | 12 0 | 4
-3 | 5 1 | 3
-2 | 0 (raiz) 2 | 0
-1 | 3 3 | 5
0 | 4 4 | 12

Equação modular: São equações que apresenta o módulo
Obs: 1º) |ax + b| = k, temos que k ≥ 0
2º) Não existe solução quando |ax + b| = - k
Seja a equação |ax + b| = k
temos ax + b = k ou
ax + b = -k
Resolver uma equação modular é encontrar valores para a incógnita que venha satisfazer na equação
1 - Resolver a equação modular
|x + 2| = 4
Condições:
1º) x + 2 = 4 ou 2º) x + 2 = – 4
Resolução:
x + 2 = 4 → x = 4 – 2 → x = 2
x + 2 = – 4 → x = – 4 – 2 → x = – 6
S = {–6; 2}
2 - Resolver a equação modular
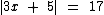
Condições:
1º) 3x + 5 = 17 ou 2º) 3x + 5 = -17
Resolução
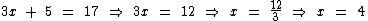
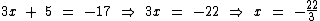
S = (-22/3 ; 4)
3 - Resolver a equação modular
|2x - 10| = 16
Condições:
2x - 10 = 16 temos 2x = 16 + 10 logo 2x = 26 assim x = 13
2x - 10 = -16 temos 2x = -16 + 10 logo 2x = -6 assim x = -3
3ª Atividade
1 - Resolva as equações modulares:
a) |x - 7| = 10 b) |2x - 10| = 2 c) |3x + 3| = 5
Inequação modular
Quando temos a inequação
|x| < a, logo x < a ou x > -a
|x | > a, logo x > a ou x < -a
Observe a resolução da inequação |x - 4 | > 10.
1º x - 4 > 10 logo x > 10 + 4 assim x > 14
2º x - 4 < -10 logo x < -10 + 4 assim x < -6
S = {x R/ x < -6 ou x > 14}
1 - Resolva as inequações modulares:
a) |2x - 3 | > 17 b) |3 + 2x| < 11
1º) Para quaisquer valores reais de x temos as seguintes propriedades:
2º) Para a e b reais temos as seguintes propriedades:
a)
b)
c)

Gráfico de uma função modular: f(x) = | x |
Gráfico da função modular: f(x) = | x | x | y
Observe: x = -2 temos f(x) = 2, -2 | 2
x = -1 temos f(x) = 1, -1 | 1
x = 1 temos f(x) = 1 0 | 0 (raiz)
x = 2 temos f(x) = 2 1 | 1
2 | 2

Observe o esboço do gráfico da função f(x) = |2x + 6|
1º -Raiz da equação 2x + 6 = 0, temos 2x = -6 teremos x = -3 Para x = -3 temos f(x) = 0
x = -4 temos f(x) = 2 x | y
x = -1 temos f(x) = 4 -5 | 4
x = 0 temos f(x) = 6 -4 | 2
-3 | 0
-2 | 2
-1 | 4
 (Foto: Colégio EEEP Antônio Valmir da SilvaVamos esboçar o gráfico de g(x) = | x² - 5x + 4|:
(Foto: Colégio EEEP Antônio Valmir da SilvaVamos esboçar o gráfico de g(x) = | x² - 5x + 4|:
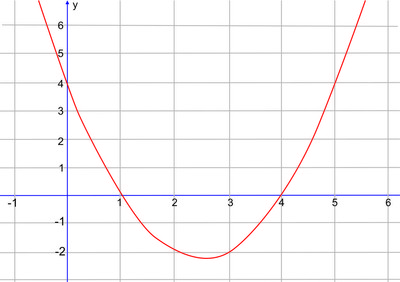
De início, o esboço do gráfico sem o módulo: h(x) = x² - 5x + 4:
Raízes da equação h(x) são 1 e 4. O valor de c é c = 4
Raízes da equação h(x) são 1 e 4. O valor de c é c = 4
 (Foto: EEEP Antônio Valmir da Silva)
(Foto: EEEP Antônio Valmir da Silva)
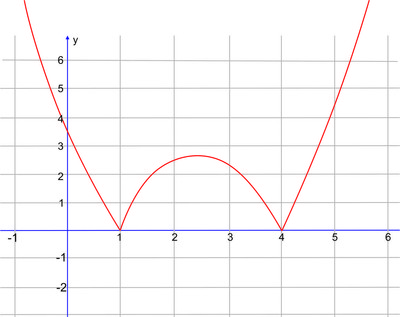
Agora aplicando o módulo (a parte que está negativa sobe), teremos o gráfico a seguir
 (Foto: EEEP Antônio Valmir da Silva)
(Foto: EEEP Antônio Valmir da Silva)Veja o gráfico da função f(x) = |x² - 4| (legal)
Raízes são x² - 4 = 0, temos que x² = 4 ou x = -2 e x = 2 (pontos no eixo x)
x | y x | y
-4 | 12 0 | 4
-3 | 5 1 | 3
-2 | 0 (raiz) 2 | 0
-1 | 3 3 | 5
0 | 4 4 | 12

2ª Atividade.
1 - Construir o gráfico da função modular f(x) = |2x - 6|, determinando o domínio e o conjunto imagem.Equação modular: São equações que apresenta o módulo
a) | x | = 4 b) | x - 2 | = 8 c) | 2x - 1 | = x + 2
Obs: 1º) |ax + b| = k, temos que k ≥ 0
2º) Não existe solução quando |ax + b| = - k
Solucionando Equações Modulares
Seja a equação |ax + b| = k
temos ax + b = k ou
ax + b = -k
Resolver uma equação modular é encontrar valores para a incógnita que venha satisfazer na equação
1 - Resolver a equação modular
|x + 2| = 4
Condições:
1º) x + 2 = 4 ou 2º) x + 2 = – 4
Resolução:
x + 2 = 4 → x = 4 – 2 → x = 2
x + 2 = – 4 → x = – 4 – 2 → x = – 6
S = {–6; 2}
2 - Resolver a equação modular
Condições:
1º) 3x + 5 = 17 ou 2º) 3x + 5 = -17
Resolução
S = (-22/3 ; 4)
3 - Resolver a equação modular
|2x - 10| = 16
Condições:
1º) 2x - 10 = 16 ou 2º) 2x - 10 = -16
Resolução2x - 10 = 16 temos 2x = 16 + 10 logo 2x = 26 assim x = 13
2x - 10 = -16 temos 2x = -16 + 10 logo 2x = -6 assim x = -3
3ª Atividade
1 - Resolva as equações modulares:
a) |x - 7| = 10 b) |2x - 10| = 2 c) |3x + 3| = 5
Inequação modular
Quando temos a inequação
|x| < a, logo x < a ou x > -a
|x | > a, logo x > a ou x < -a
Observe a resolução da inequação |x - 4 | > 10.
1º x - 4 > 10 logo x > 10 + 4 assim x > 14
2º x - 4 < -10 logo x < -10 + 4 assim x < -6
S = {x R/ x < -6 ou x > 14}
4ª Atividade
1 - Resolva as inequações modulares:
a) |2x - 3 | > 17 b) |3 + 2x| < 11

















