FUNÇÃO EXPONENCIAL
Definição de Função Exponencial
São funções f: R→R tal que f(x) = a x, sendo que a > 0 e a ≠ 1 e x um número real
A lei de formação de uma função exponencial indica que a base elevada ao expoente x precisa ser maior que zero e diferente de um.
Uma função pode ser representada através de um gráfico, e no caso da exponencial, temos duas situações:
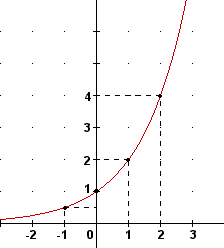
1º caso: a > 1 (base maior que 1)
2º caso: 0 < a < 1. (base maior que zero e menor que 1)
Observe como os gráficos são constituídos respeitando as condições propostas
: Traçar o gráfico das funções f(x) = 2x (crescente) e f(x) = (1/2)x (decrescente), para isso vamos dar valores para "x" e achar seu correspondente em "y":
Traçar o gráfico das funções f(x) = 2x (crescente) e f(x) = (1/2)x (decrescente), para isso vamos dar valores para "x" e achar seu correspondente em "y":
y = 2x
x
y
-1
2-1=1/2
0
20=1
1
21=2
2
22=4
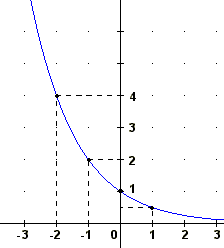
f(x) = (1/2) x
x
y
-2
(1/2)-2 =4
-1
(1/2)-1 =2
0
(1/2)0 =1
1
(1/2)1 =1/2
1ª Atividade
1 - Construa o gráfico da função exponencial.
a) f(x) = 4x
2 - Considerando que f(x) = 49x, determine o valor de f(1,5).
3 - Dadas as funções f(x) = 2 x² – 4 e g(x) = 4 x² – 2x, se x satisfaz f(x) = g(x), então determine 2x
Definição de Função Exponencial
São funções f: R→R tal que f(x) = a x, sendo que a > 0 e a ≠ 1 e x um número real
A lei de formação de uma função exponencial indica que a base elevada ao expoente x precisa ser maior que zero e diferente de um.
Uma função pode ser representada através de um gráfico, e no caso da exponencial, temos duas situações:
1º caso: a > 1 (base maior que 1)
2º caso: 0 < a < 1. (base maior que zero e menor que 1)
Observe como os gráficos são constituídos respeitando as condições propostas
:

Traçar o gráfico das funções f(x) = 2x (crescente) e f(x) = (1/2)x (decrescente), para isso vamos dar valores para "x" e achar seu correspondente em "y":
y = 2x
 |
f(x) = (1/2) x
 |
1ª Atividade
1 - Construa o gráfico da função exponencial.
a) f(x) = 4x
2 - Considerando que f(x) = 49x, determine o valor de f(1,5).
3 - Dadas as funções f(x) = 2 x² – 4 e g(x) = 4 x² – 2x, se x satisfaz f(x) = g(x), então determine 2x
Aplicação da Função Exponencial no cotidiano
NÃO copiar
Uma função exponencial é utilizada na representação de situações em que a taxa de variação é considerada grande, por exemplo, em rendimentos financeiros capitalizados por juros compostos, no decaimento radioativo de substâncias químicas, desenvolvimento de bactérias e micro-organismos, crescimento populacional entre outras situações.
As funções exponenciais devem ser resolvidas utilizando, se necessário, as regras envolvendo potenciação.
Função Exponencial na Matemática Financeira
Uma expressão matemática utilizada no cálculo dos juros compostos é a seguinte:
M = C * (1 + i)t, onde o capital C é multiplicado pela exponencial
M: montante
C: capital
i: taxa de juros
t: tempo de aplicação
1 - Num depósito a prazo efetuado em um banco, o capital acumulado ao fim de certo tempo é dado pela fórmula C = D * (1 + i)t, onde C representa o capital acumulado, D o valor do depósito, i a taxa de juros ao mês e t o tempo de meses em que o dinheiro está aplicado. Nesse sistema, ao final de cada mês os juros capitalizados são incorporados ao depósito.
a) Para um depósito de R$ 1 000,00, com taxa de 2% ao mês, qual o capital acumulado ao fim de 6 meses?
M = C * (1 + i)t, onde o capital C é multiplicado pela exponencial
M: montante
C: capital
i: taxa de juros
t: tempo de aplicação
1 - Num depósito a prazo efetuado em um banco, o capital acumulado ao fim de certo tempo é dado pela fórmula C = D * (1 + i)t, onde C representa o capital acumulado, D o valor do depósito, i a taxa de juros ao mês e t o tempo de meses em que o dinheiro está aplicado. Nesse sistema, ao final de cada mês os juros capitalizados são incorporados ao depósito.
a) Para um depósito de R$ 1 000,00, com taxa de 2% ao mês, qual o capital acumulado ao fim de 6 meses?
C = D * (1 + i)t
C = 1000 * (1 + 0,02)6
C = 1000 * 1,026
C = 1000 * 1,126162419264
C = 1 126,16
O capital acumulado será de R$ 1.126,16.
b) Para um depósito de R$ 5 000,00, a uma taxa de 5% ao mês, qual o capital acumulado durante 4 meses?
C = D * (1 + i)t
C = 5000 * (1 + 0,05)4
C = 5000 * 1,054
C = 5000 * 1,21550625
C = 6 077,53
O capital acumulado será de R$ 6.077,53.
c) Para um depósito de R$ 2 500,00, a uma taxa de juros de 10% ao ano, qual será o capital acumulado durante 10 anos?
C = D * (1 + i)t
C = 2500 * (1 + 0,1)10
C = 2500 * 1,0110
C= 2500 * 2,5937424601
C = 6484,36
O capital acumulado em 10 anos será de R$ 6.484,36.
Função Exponencial na Física
A função exponencial é utilizada para calcular a desintegração das substâncias radioativas através da equação (1):
 em que y0 é a quantidade inicial, correspondente ao momento t = 0.
em que y0 é a quantidade inicial, correspondente ao momento t = 0.
Por exemplo, sabe-se que em 5730 anos metade do carbono 14 decompõe-se. De acordo com estes dados, vamos calcular o valor da constante k da expressão (1).
Temos que t = 5730 anos,
 e que
e que
 com estes dados chegamos a
com estes dados chegamos a
 então no caso concreto do carbono 14 temos a seguinte fórmula
então no caso concreto do carbono 14 temos a seguinte fórmula

Por exemplo, sabe-se que em 5730 anos metade do carbono 14 decompõe-se. De acordo com estes dados, vamos calcular o valor da constante k da expressão (1).
Temos que t = 5730 anos,

Vamos apresentar alguns exemplos envolvendo o uso de Funções Exponenciais.
Exemplo 1
(Unit-SE) Uma determinada máquina industrial se deprecia de tal forma que seu valor, t anos após a sua compra, é dado por v(t) = v0 * 2 –0,2t, em que v0 é uma constante real. Se, após 10 anos, a máquina estiver valendo R$ 12 000,00, determine o valor que ela foi comprada.
Temos que v(10) = 12 000, então:
v(10) = v0 * 2 –0,2*10
12 000 = v0 * 2 –2
12 000 = v0 * 1/4
12 000 : 1/ 4 = v0
v0 = 12 000 * 4
v0 = 48 000
Exemplo 1
(Unit-SE) Uma determinada máquina industrial se deprecia de tal forma que seu valor, t anos após a sua compra, é dado por v(t) = v0 * 2 –0,2t, em que v0 é uma constante real. Se, após 10 anos, a máquina estiver valendo R$ 12 000,00, determine o valor que ela foi comprada.
Temos que v(10) = 12 000, então:
v(10) = v0 * 2 –0,2*10
12 000 = v0 * 2 –2
12 000 = v0 * 1/4
12 000 : 1/ 4 = v0
v0 = 12 000 * 4
v0 = 48 000
A máquina foi comprada pelo valor de R$ 48 000,00.
Exemplo 2
(EU-PI) Suponha que, em 2003, o PIB (Produto Interno Bruto) de um país seja de 500 bilhões de dólares. Se o PIB crescer 3% ao ano, de forma cumulativa, qual será o PIB do país em 2023, dado em bilhões de dólares? Use 1,0320 = 1,80.
Temos a seguinte função exponencial
P(x) = P0 * (1 + i)t
P(x) = 500 * (1 + 0,03)20
P(x) = 500 * 1,0320
P(x) = 500 * 1,80
P(x) = 900
P(x) = 500 * (1 + 0,03)20
P(x) = 500 * 1,0320
P(x) = 500 * 1,80
P(x) = 900
O PIB do país no ano de 2023 será igual a R$ 900 bilhões.
2ª Atividade
Equações exponenciais
1 - Resolva as equações exponenciais
a) 
b) 5 x + 3 . 5 x + 2 . 5 x = 125
c) 2 3x – 2 . 8 x + 1 = 4 x – 1
d) 24x + 1 . 8 –x + 3 = 16 –1
e) 
2 - Resolva as inequações exponenciais
a) 2 3x – 2 > 16 b) 1/4 < (1/2) 3x – 2
3 - A quantia de R$ 1200,00 foi aplicada em uma instituição bancária a uma taxa de 1,5% ao mês, no sistema de juros compostos. (Use: (1,015) 12 =1,19)
a) Qual será o montante no final de 12 meses?
Nenhum comentário:
Postar um comentário