Potenciação
Note que temos o número dois ( base ) com o número três (expoente) sobrescrito à sua direita ( 23 ).
Dizemos que o número 2 está elevado à terceira potência, ou ainda que 23 é a terceira potência de 2.
Nesta potência o número 2 é a sua base e ao número 3 é o expoente.
Esta potência representa a multiplicação de três fatores iguais a dois, então 23 é igual a 2 . 2 . 2 que é igual a 8.
Potências com expoente 2 ou 3 possuem uma outra forma particular de leitura. A potência 23 também pode ser lida como dois ao cubo, assim como a potência 32 pode ser lida como três ao quadrado.
Potências de Base Real com Expoente Inteiro
Nestas condições há quatro situações em particular que iremos tratar. A saber, quando o expoente é maior que um, quando é igual a um, quando é igual a zero e quando é negativo.
Expoente maior que 1
De forma geral:
Este é o caso de mais fácil compreensão, pois o conceito da exponenciação está bem claro. Observe a expressão abaixo:
Expoente igual a 1
Todo número elevado a 1 é igual ao próprio número:
Expoente igual a 0 (zero)
Todo número, diferente de zero, elevado a 0 é igual a 1:
Obs: 00 é indeterminado, embora em algumas situações convenciona-se que seja igual a 1. Para qualquer outro expoente real n positivo, temos que 0n = 0.
Expoente negativo
Qualquer número diferente de zero elevado a um expoente negativo é igual ao inverso deste número elevado ao oposto do expoente:
Vejamos agora a explicação onde se baseiam estes três últimos conceitos explicados acima.
Propriedades das potências de base real com expoente inteiro
Multiplicação de potências de mesma base
A multiplicação de potências de mesma base é igual a esta base elevada à soma dos expoentes.
Generalizando:
Divisão de potências de mesma base
A divisão de potências de mesma base, diferente de zero, é igual a esta base elevada à diferença dos expoentes.
Generalizando temos:
Note que a base a deve ser diferente de 0, pois como sabemos não existe quociente real para a divisão por zero neste conjunto numérico.
Obs: a0 = 1
Para todo número a real, com a diferente de zero, temos:
É por isto que todo número, diferente de zero, elevado a 0 é igual a 1:
Potência de um produto
A potência do produto de dois ou mais fatores é igual ao produto de cada um destes fatores elevados ao expoente em questão:
Vamos tomar como exemplo o produto de três fatores distintos elevados ao cubo:
Não custa nada fazermos uma verificação só para conferir:
Potência de um quociente
Podemos proceder de forma análoga ao que fizemos no caso da multiplicação, mas neste caso os divisores não podem ser iguais a zero:
Potência de um expoente fracionário
Podemos transformar uma potência com expoente fracionário em um radical:
Exemplo:
Potência de uma potência
Novamente para uma base diferente de zero podemos expressar a seguinte igualdade:
Vamos como de costume recorrer a um exemplo:
E agora vamos verificar a veracidade desta propriedade:
1ª Atividade
1 - Calcule:
a) 33 + 23 c)(2/3)3 c) (- 2)3 - (-2)3
2 - Aplicando as propriedades, determine:
a) (23).(24).(2-5) b) (103).(10-4).(1010)
3) Calcule:
a) 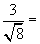 b)
b) 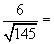 c)
c) 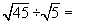
Desafios curiosos - NÃO precisa copiar
Cozinhar um bolo
1 - Como medirias os 11 minutos que são
necessários para cozinhar um bolo, com duas
ampulhetas de 8 e 5 minutos respectivamente?



2 - Buscando água, uma rã caiu em um poço de 30
metros de profundidade. Na sua busca por
sobrevivência, a obstinada rã conseguia subir 3
metros cada dia, sendo que a noite resbalava e
descia 2 metros. Quantos dias a rã demorou para sair
do poço?

3 - Dois pais e dois filhos foram pescar. Cada um pescou um peixe, sendo que ao todo foram pescados 3 peixes. Como isso é possível?
5 - O vovô "Controlado" tinha muitos netos. No
Natal, resolveu presenteá-los com um dinheirinho.
Separou uma quantia em dinheiro e percebeu que, se
ele der R$12,00 a cada garoto, ainda ficará com R$
60,00. Se ele der R$15,00 a cada um, precisará de
mais R$ 6,00. Quantos netos o vovô
"Controlado" tem?
Natal, resolveu presenteá-los com um dinheirinho.
Separou uma quantia em dinheiro e percebeu que, se
ele der R$
60,00. Se ele der R$
mais R$ 6,00. Quantos netos o vovô
"Controlado" tem?
6 - Divida o vinho entre os viajantes
Dois amigos bêbados compraram 8 litros de vinho. Eles estavam caminhando, e na metade do caminho, decidem separar-se, repartindo antes o vinho igualmente.
Para realizar as medidas há um barril de 8 litros (onde está o vinho), uma vasilha de 5 e outra de 3 litros. Como eles podem fazer para repartir igualmente o vinho?

7 - Uma garrafa com sua tampa custa R$ 1,10. Sabendo que a garrafa custa R$ 1,00 a mais que a tampa, qual é o preço da tampa da garrafa? E qual é o preço da garrafa?
8 - Os Relógios
Um homem tem dois relógios. Um deles não anda e o outro
atrasa uma hora por dia. Qual deles mostrará mais
freqüentemente a hora certa?
9 - Elevei um número positivo ao quadrado, subtraí do resultado o mesmo número e o que restou dividi ainda pelo mesmo número. O resultado que achei foi igual:
a) Ao próprio número
b) Ao dobro do número
c) Ao número mais 1
d) Ao número menos 1
b) Ao dobro do número
c) Ao número mais 1
d) Ao número menos 1
10 - A matemática e a música

11 -

12 -

13 -

14 -
Origem dos algarismos Indu-arábicos

15 -
Você acha fácil dobrar uma folha de papel? Que tal tentar dobrá-la 50 vezes?
Aqui está a folha... | Dobrando 1 vez... |
Dobrando 2 vezes... | Dobrando 3 vezes... |
Dobrando 4 vezes... | Dobrando 5 vezes... |
Dobrando 6 vezes... | ... |
Você pode até conseguir dobrar 7 ou 8 vezes, mas nada além disso. Porém, por incrível que pareça, se você conseguisse dobrar a folha 50 vezes, ela apresentaria uma espessura aproximadamente igual à distância da Terra à Lua.
Observação: para dobrar uma folha 50 vezes ela deveria ter mais de 4.000.000 Km de comprimento!
16 -
Vamos imaginar que dobramos um enorme
pedaço de papel ao meio. Depois dobramos
mais uma vez, e outra vez, e assim por diante.
Quantas vezes conseguimos dobrar o nosso
pedaço de papel?
.
Normalmente conseguimos dobrar uma folha
A4 apenas 6 vezes e dificilmente se
consegue dobrar um pedaço maior mais do
que 7 vezes. Experimentem!
.
Mas vamos imaginar que conseguimos
Mas vamos imaginar que conseguimos
dobrar um pedaço de papel 51 vezes. No final
qual seria a espessura do nosso papel? Dez
centímetros? 50 centímetros? Um metro?
Cinquenta metros? Um quilômetro?
.
A resposta é mais de 150.000.000 km! Sim,
A resposta é mais de 150.000.000 km! Sim,
cento e cinquenta milhões de quilômetros! No
final obteríamos uma torre que se estenderia
para lá do Sol!
.
Quando dobramos o papel a primeira vez
.
Quando dobramos o papel a primeira vez
obtemos uma espessura duas vezes maior do
que a da folha inicial. Quando dobramos a
segunda vez será quatro vezes mais espesso.
Cada vez que dobramos uma vez duplicamos
a espessura em relação ao dobramento
anterior. Depois dos primeiros dobramentos
os números tornam-se imediatamente muito
grandes. Vamos ver como:
.
.
Primeira dobra...2 folhas
Segunda dobra... 4 folhas
3ª - 8 folhas
4ª - 16 folhas
5ª - 32 folhas
6ª - 64 folhas
7ª - 128 folhas
8ª - 256 folhas
………….
40ª - 1.000.000.000.000 folhas
…………
50ª - 1.000.000.000.000.000 folhas
(espessura=100.000.000 km)
51ª – Espessura = 200.000.000 km
.
E passamos o Sol!
.
(Distância da Terra ao Sol = 149.597.871 km

Nenhum comentário:
Postar um comentário