Função do 2º Grau

Definição

Função Polinomial do 2º Grau ou Função Quadrática é a função real definida por: f(x) = ax² + bx + c, onde a, b e c são coeficientes reais, sendo a ≠ 0.

Vejamos alguns exemplos de função quadrática:
a) y = x²2 – 5x + 6, na qual a = 1, b = -5 e c = 6 b) y = - x²+ x , na qual a = - 1, b = 1 e c = 0

c) y = 3x2 – 4x, na qual a = 3, b = -4 e c = 0
d) y = 2x2 – 1, na qual a = 2, b = 0 e c = -1

As raízes da função f(x) = ax² + bx + c, são obtidas através da fórmula de Bhaskara (Raízes da função)

onde

é denominado discriminante de f(x).

O gráfico da função e as raízes

A parábola corta o eixo do x nas raízes e o eixo y no valor de c.

Concavidade da parábola

A parábola pode ter a concavidade voltada para cima ou para baixo.
A parábola tem a concavidade voltada para cima quando a > 0 enquanto tem a concavidade voltada para baixo quando a < 0.

a > 0 a < 0

Obs: A parábola pode cortar ou não o eixo x (a > 0)

duas raízes reais (dois pontos no eixo x)

(a > 0) duas raízes reais e iguais ( um único ponto no eixo x)

Delta < 0 Não há raízes reais (a parábola não corta o eixo x)

O valor de c no plano cartesiano

Resumindo

VÉRTICE DA PARÁBOLA:

O vértice da parábola determina o ponto de mínimo (a > 0) ou de máximo da função (a < 0). Tal vértice será o par ordenado (x_v,y_v).

Valor mínimo (a > 0)

Valor máximo (a < 0)

Fórmulas para calcular as coordenadas do vértice.

Observe bem aluno(a)s do TE1 e TEM 1

Conjunto imagem da função quadrática.

O conjunto imagem é determinada no eixo y do plano cartesiano
1º - Se a parábola está voltada para baixo (a < 0) a imagem da função é
Im(f) = {y

R/ y

Yv}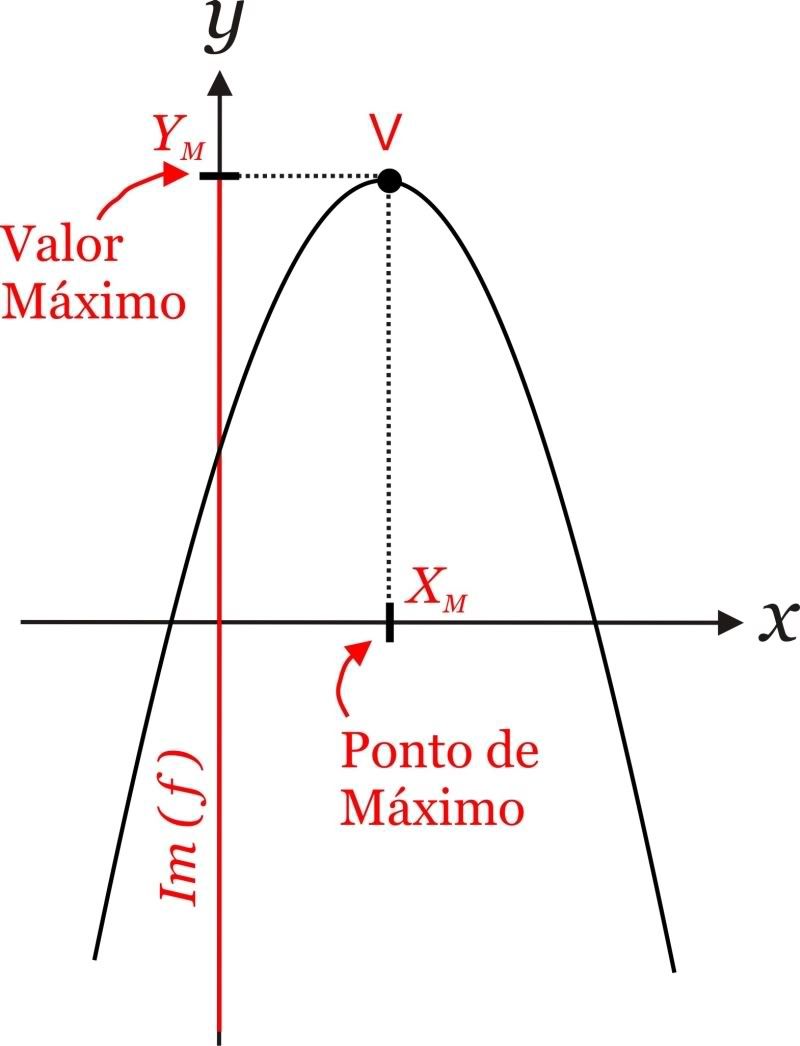

2º - Se a parábola está voltada para cima (a > 0) a imagem da função é
Im(f) = {y

R/ y > Yv}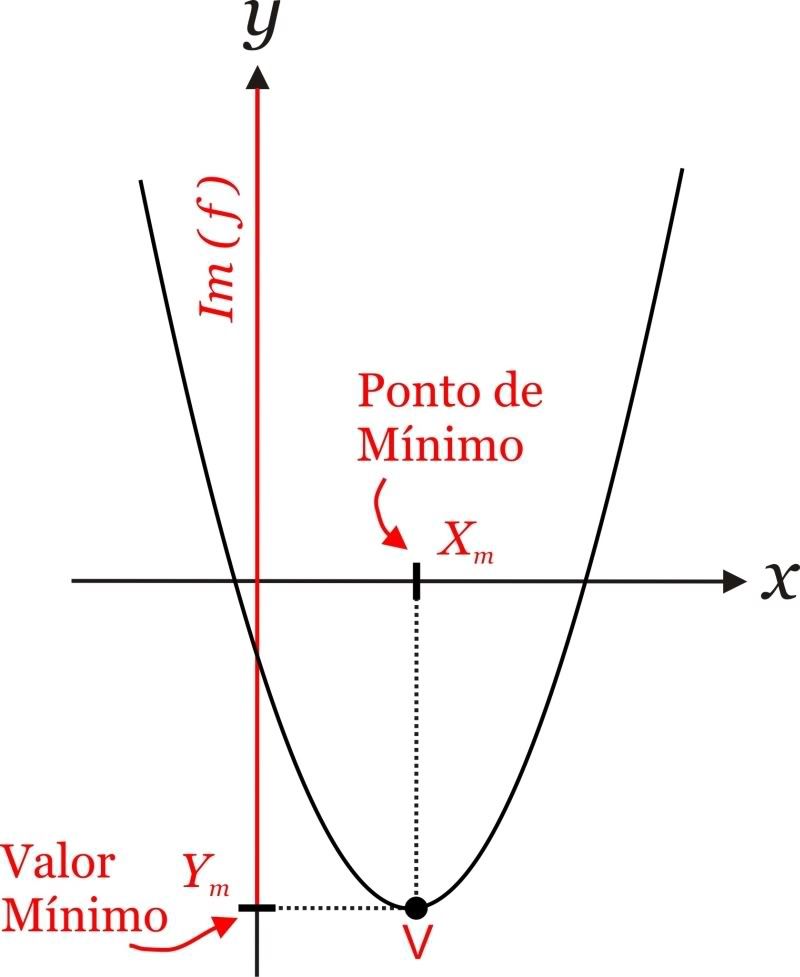

Assim para determinar o conjunto imagem da função é preciso determinar o

Ex: 1 - O conjunto imagem da função f(x) = x² - 8x + 12 é
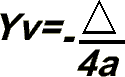
Im(f) = {y

R/ y > -4}

Observe as questões resolvidas

Atividade NÃO copiar

1 - Determinar as raízes da função

a) f(x) = x² - 10x + 16 b) f(x) = 3x² - 48x c) f(x) = 2x² - 32

2 Determine as coordenadas do vértice das funções quadráticas:

a) f(x) = 2x² - 4x + 2 b) f(x) = 3x² - 6x - 1

c) f(x) = x² - 4x - 3 d) f(x) = - 2x² + 8x

3 - Determine o conjunto imagem das funções:

a) f(x) = x² - 6x + 5 b) f(x) = - x²  + 6x - 8 c) f(x) = - x² + 4x

4 - Dada a função quadrática f(x) = - x²  + 11x - 18, determine
a) a soma e o produto das raízes
b) as raízes da função
c) as coordenadas do vértices da função
d) o conjunto imagem da função
e) a representação gráfica da função

5 - Represente no plano cartesiano o gráfico das funções:
a) f(x) = x² - 4x + 4 b) f(x) = - x²  + 5x.

Exercício - É para copiar e resolver TE 1 e TEM 1 em 08/05/15

1 - Claudete leu 3/5 de um livro e ainda faltam 68 páginas para ela terminar de ler o livro todo. Quantas páginas têm o livro?

2- Um copo cheio de água pesa 425g. Se jogarmos metade da água fora, seu peso cai para 280 g. O peso do copo vazio é:

3 - Na compra de um carro, foi dada uma entrada, correspondendo a um terço do seu valor, e o restante foi financiado em 24 prestações fixas de R$ 625,00. Calcule o preço do carro.

4 - Um pai querendo incentivar o filho a estudar
matemática, combina pagar-lhe R$ 8,00 por problema que ele acertar, mas vai cobrar R$ 5,00 por problema que ele errar. Depois de 26 problemas fazem as contas e o filho nada recebe e nada deve. Quantos problemas ele acertou?

Curiosidade NÃO É PARA COPIAR - Veja essas curiosidades

1 - Escolha um numero de três algarismos:
Ex: 234
Repita este numero na frente do mesmo:
234234
Agora divida por 13:
234234 / 13 = 18018
Agora divida o resultado por 11:
18018 / 11 = 1638
Divida novamente o resultado, só que agora por 7:
1638 / 7 = 234
O resultado é igual ao numero de três algarismos que você havia escolhido: 234.
__________________________________________________
2 - Você sabia que adicionando o número 1 à multiplicação de quatro números consecutivos você obtém um quadrado perfeito?
Exemplo: 1*2*3*4+1 = 25
4 * 5 * 6 * 7 + 1 = 841 que equivale a 29²
^{8 * 9 * 10 * 11 + 1 = 7921 que equivale a}89²
^{E assim por diante}
_________________________________________________
3 - Você acha fácil dobrar uma folha de papel? Que tal tentar dobrá-la 50 vezes?

Aqui está a folha...	Dobrando 1 vez...

Dobrando 2 vezes...	Dobrando 3 vezes...

Dobrando 4 vezes...	Dobrando 5 vezes...

Dobrando 6 vezes...	...

Você pode até conseguir dobrar 7 ou 8 vezes, mas nada além disso. Porém, por incrível que pareça, se você conseguisse dobrar a folha 50 vezes, ela apresentaria uma espessura aproximadamente igual à distância da Terra à Lua.
Observação: para dobrar uma folha 50 vezes ela deveria ter mais de 4.000.000 Km de comprimento!
________________________________________________

4 - Considerando o dia 4 de Maio de 2006, aos 2 minutos e 3 segundos passados da 1 hora da manhã, temos o seguinte horário seqüencial:

01:02:03 04/05/06
É uma seqüencia numérica que jamais irá se repetir.

5 - Você sabe o que é ano-luz? É uma unidade de comprimento ou a distância que a luz percorre num período de tempo de um ano. A luz desenvolve uma velocidade de aproximadamente 300.000 km/s. Ou seja, em 1 segundo a luz percorre uma distância de 300.000 km. Se a luz percorre 300.000 km em 1 segundo, em 1 ano a luz percorre uma distância de 9.460.800.000.000 Km, mais de 9 trilhões de quilômetros em um ano! Dessa forma, quando ouvimos falar que foi descoberta uma nova galáxia que está localizada, por exemplo, a 10 anos-luz de distância da Terra, significa que ela está a uma distância de 90 trilhões de quilômetros.
_______________________________________________
6 -

1 x 1 = 1

11 x 11 = 121

111 x 111 = 12321

1111 x 1111 = 1234321

11111 x 11111 = 123454321

111111 x 111111 = 12345654321

1111111 x 1111111 = 1234567654321

11111111 x 11111111 = 123456787654321

111111111 x 111111111 = 12345678987654321

____________________________________________

7 -

9 x 9 + 7 = 88

98 x 9 + 6 = 888

987 x 9 + 5 = 8888

9876 x 9 + 4 = 88888

98765 x 9 + 3 = 888888

987654 x 9 + 2 = 8888888

9876543 x 9 + 1 = 88888888

98765432 x 9 + 0 = 888888888

___________________________________________

8 - Apesar de não ser a verdadeira história da origem destes

números não deixa de ser bastante interessante e curiosa.

Coincidências ;-)

Os números 1,2,3 e 4

Os números 5, 6, 7 e 8

O número 9

O mais interessante de todos! O número 0!

____________________________________________________________________________

9 - Você conhece o número mágico?

O número é 1089 é conhecido como o número mágico. Veja

porque:

1 - Escolha qualquer número de três algarismos distintos:

por exemplo, 875.

Agora escreva este número de trás para frente e subtraia o

menor do maior:

875 - 578 = 297

Agora inverta também esse resultado e faça a soma:

297 + 792 = 1089 (o número mágico)

2 - Digamos que o número seja 743. Escrevendo ao

contrário 347, subtraindo 743 - 347 = 396

Agora somando 396 + 693 = 1089 (Agora é com você)

_____________________________________________

10 - Você sabia que a fórmula para resolver uma equação do 3º grau do tipo x³+ px + q = 0 é a seguinte

______________________________________________

11 - O maior número primo conhecido é 2^32.582.657-1, que tem 9.808.358 dígitos e foi descoberto em 4/9/2006 pelos Drs. Curtis Cooper, Steven Boone e sua equipe. Este primo tem 650.000 dígitos a mais do que o maior primo encontrado por eles mesmos em dezembro de 2005.

____________________________________________________________________________________

12 - Número primo

_________________________________________________

13 - O valor de pi é aproximado

As questões a seguir são questões de aplicação de função do 2º grau

O aluno(a) é quem escolhe em copiar ou não. Você decide

1 - O diretor de uma orquestra percebeu que, com o

ingresso a R$ 9,00, em média 300 pessoas assistem aos

concertos e que, para cada redução de R$ 1,00 no preço

dos ingressos, o público aumenta de 100 espectadores.

Qual deve ser o preço do ingresso para que a receita seja

máxima? (Obs: Construir o gráfico)

2 - O movimento de um projétil, lançado para cima

verticalmente, é descrito pela equação y = – 40x² + 200x.

Onde y é a altura, em metros, atingida pelo projétil x

segundos após o lançamento. A altura máxima atingida e o

tempo que esse projétil permanece no ar correspondem,

respectivamente, a: (Obs: Construir o gráfico)

a) 6,25 m, 5s b) 250 m, 0 s c) 250 m, 5s

d) 250 m, 200 s e) 10.000 m , 5s

3 - Para pagar as despesas mensais de um condomínio,

ficou combinado que todos contribuiriam com a mesma

quantia. Num certo mês, em que as despesas totalizaram

R$ 360,00, devido à inadimplência de dois dos

condôminos, cada um dos demais foi obrigado a pagar,

além da sua

cota normal, um adicional de R$ 6,00. Qual é o número de

condôminos? (Obs: Construir o gráfico).

4 - Para pagar as despesas mensais de um condomínio,

ficou combinado que todos contribuiriam com a mesma

quantia. Num certo mês, em que as despesas totalizaram

R$ 600,00, devido à inadimplência de 4 dos condô-minos,

cada um dos demais foi obrigado a pagar, além da sua

cota normal, um adicional de R$ 5,00. Qual é o número de

condôminos? (Obs: Construir o gráfico).

5 - Um computador devia ser comprado por um grupo de

pessoas que contribuíam em partes iguais. Como 4 delas

desistiram, a quota de cada um aumentou em R$ 15,00.

Quantas eram as pessoas? (Construir o gráfico)

6 - Duas torneiras enchem um tanque em 6 horas. A

primeira gasta 5 horas a mais para encher esse tanque do

que a segunda.. Quanto tempo gastará a segunda

torneira,

isoladamente, para encher esse tanque?

Matemática - Prof. César Ferreira

quarta-feira, 18 de junho de 2014